Déplacements et isométries du plan

Parmi les isométries du plan on peut distinguer celles qui conservent l'orientation (déplacements) et celles qui inversent l'orientation (antidéplacements ou retournements)

Déplacements

Commençons par les déplacements. Ils sont de deux types:

• les rotations (c'est le cas général)
• les translations

Se donner un point p et son image p' est évidemment insuffisant. Il existe bien des rotations amenant p sur p' . On peut préciser en donnant une demi-droite D issue de p et son image D' (une demi-droite issue de p' ). Dès lors le déplacement est bien déterminé.

Remarquons que la donnée de l'image d'un point et d'une demi-droite est équivalente à se donner deux points p , q et leurs images p' , q' (avec pq = p'q' ); ces données sont souvent plus aisées à manier. 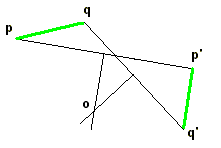Comment trouver le déplacement amenant pq sur p'q' ? Le centre de la rotation est situé sur la médiatrice de pp' . Il se trouve également sur celle de qq' . C'est donc le point d'intersection o de ces deux droites. Toutefois le raisonnement est un peu rapide. En effet est-on assuré que ces deux droites se coupent en un point? Elles pourraient être parallèles, voire confondues. Nous devons examiner ces cas séparément. Qu'elles soient parallèles ou confondues, cela signifie que pp' et qq' sont également parallèles. De plus pq = p'q' . Le quadrilatère pp'q'q est donc soit un trapèze isocèle, soit un parallélogramme.

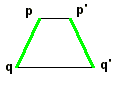
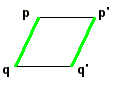
Dans le cas d'un trapèze isocèle il s'agit d'une rotation ayant pour centre le point d'intersection des côtés non-parallèles. Si c'est un parallélogramme il s'agit d'une translation d'amplitude pp'

Antidéplacements

Les antidéplacements sont moins bien connus que les déplacements. Pourtant c'est aussi simple; il y en a deux classes:

• les symétries glissées (cas général)
• les symétries axiales

Une symétrie glissée est généralement décrite comme une symétrie axiale suivie (ou précédée, c'est commutatif) d'une translation parallèle à l'axe de symétrie. C'est la complication de cette définition qui fait que d'habitude on ne s'intéresse guère aux symétries glissées "puisque c'est la composée de deux transformations". Cet argument est évidemment stupide puisqu'une rotation peut également s'obtenir comme produit de deux transformations (symétries axiales).

Une manière simple de se représenter cette transformation est de regarder des traces de pas dans la neige. Pour mieux sentir qu'il s'agit d'"une" transformation, on peut couper en son milieu un bouchon. Le tire-bouchon, en vissant, a laissé comme empreinte dans un plan médian une symétrie glissée; c'est la trace, dans le plan, d'un mouvement hélicoïdal.

Dans un antidéplacement l'orientation est inversée. Tout comme un déplacement, il est déterminé par la donnée d'une demi-droite D issue d'un point p et de son image D' (demi-droite issue de p' ). Comme plus haut on peut également se donner deux points p , q et leurs images p' , q' (avec pq = p'q' ).

Comment trouver la symétrie (glissée ou non) qui correspond à cet antidéplacement ? 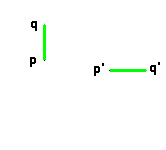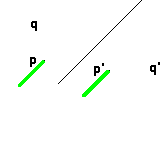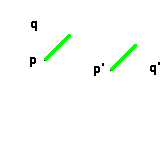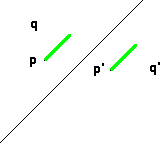Si le segment pq tourne autour du point p , l'image, le segment p'q' , tourne autour de p' , mais en sens inverse (il s'agit d'un antidéplacement, on change l'orientation). Donc il existera deux positions (opposées) où le vecteur pq sera parallèle au vecteur p'q' . Il suffit alors de prendre la parallèle à cette direction passant par le milieu de pp' . Ce sera l'axe de la symétrie; on voit immédiatement que l'amplitude de la translation est égale à la projection de pp' sur l'axe de la symétrie glissée.

Donc en résumé, nous avons la situation suivante:

Isométries du plan
Déplacements		Antidéplacements
Rotations	Translations	Symétries glissées	Symétries axiales

C'est quoi un groupe de permutations ?

À plusieurs reprises, nous avons utilisé le terme groupe sans le définir. Dans son sens usuel ce serait tout simplement un ensemble; mais quand les mathématiciens parlent de groupe ils y voient un ensemble possédant de belles propriétés.

Considérons un ensemble de permutations, par exemple un ensemble d'isométries. Une figure et sa transformée seront dites équivalentes; dans l'exemple on dira isométriques. Mais pour que les choses fonctionnent correctement il faut que deux figures équivalentes à une même troisième soient équivalentes entre elles. C'est, dans le cas des isométries, un des axiomes d'Euclide.

Cette exigence a des implications sur l'ensemble de permutations considéré. En effet si deux figures F ₁ et F ₂ sont équivalentes à une même figure F (c'est-à-dire que ces figures soient les transformées de F par deux permutations P ₁ et P ₂ ) on souhaite que F ₁ et F ₂ soient équivalentes c'est-à-dire qu'il existe parmi les permutations de l'ensemble une permutation qui applique F ₁ sur F ₂ . Une telle permutation peut être obtenue en composant celle appliquant F ₁ sur F avec celle appliquant F sur F ₂.

Il faut donc qu'étant données deux permutations quelconques P₁ et P₂, la permutation obtenue en composant la permutation inverse de P₁ avec P₂, c'est-à-dire la permutation P₂ P₁^-1, appartienne à l'ensemble. Si cette condition est toujours vérifiée, quelles que soient les deux permutations P₁ et P₂, on dit qu'il s'agit d'un groupe de permutations.

Cette définition a de nombreuses conséquences. Par exemple :

• si on prend P₁ = P₂, on obtient la permutation identique Iqui soit appartenir à l'ensemble.
• si on prend P₂ = I, on obtient la permutation inverse P₁^-1 qui appartient également à l'ensemble.
• étant donnée la permutation P₃, si on prend P₁ = P₃^-1, la permutation composée P₂ P₃ appartient à l'ensemble.

On peut évidemment utiliser ces conséquences pour formuler des définitions équivalentes d'un groupe de permutations. Mais l'essentiel est de sentir qu'un groupe de permutations est un ensemble "harmonieux", "cohérent", "complet", ... de permutations. Après tout, avez-vous besoin d'une définition précise pour savoir ce qu'est un chien ?...

Transformée d'une permutation

Soit un permutation P que nous souhaitons transformer par la permutation T . Est-il difficile de voir le résultat ? Pas du tout et, en tout cas c'est bien plus simple que de déterminer la composée de P avec T .

Prenons un exemple.

P est une rotation de 45° autour du point p et T est une rotation de 60° autour du point t . La transformée de P par T est tout simplement la rotation P' de 45° dont le centre est le point p' transformé de p par T . Comment exprimer P' en fonction de P et T ?

Si on cherche la transformée d'une figure F, on peut se ramener à la figure transformée de F par T^-1, ensuite effectuer la permutation P et enfin transformer le résultat par T. En fin de compte on a effectué la permutation T P T^-1. Cette expression "compliquée" masque une réalité simple. C'est pourquoi on la note plutôt P^T

Si vous n'êtes pas convaincus, essayez de trouver la composée des deux rotations mentionnées plus haut (c'est évidemment une rotation de 45° + 60°), mais où est son centre...?

Cette notion simple de transformée s'avère être un outil très efficace dans l'étude des groupes de permutations, puis qu'évidemment la transformée d'un permutation du groupe par une autre doit également appartenir au groupe.

Groupes cristallographiques

Translations d'un groupe cristallographique

Ces groupes d'isométries sont ainsi dénommés car leur classification résulte d'un problème physique, celui de la classification des cristaux. On remarque en effet que dans les cristaux on trouve périodiquement les mêmes structures atomiques répétées par translation. C'est cette caractéristique qui est utilisée pour définir un groupe cristallographique.

Un groupe cristallographique du plan contient des translations dans au moins deux directions différentes (puisqu'on va remplir un plan), mais comme les pièces, morceaux de plan, qui vont se répéter ne se chevauchent pas, les translations doivent être telles qu'étant donné un point et tous ses transformés, chacun doit pouvoir être isolé (dans un petit cercle par exemple); les mathématiciens parlent alors d'un groupe discret de translations.

Cet ensemble de translations peut dans certains cas être complété par d'autres isométries: rotations, symétries glissées ou symétries axiales.

Quelles translations ?

D'après ce que nous venons de dire les images d'un point p par les isométries sont toutes isolées. Limitons nous pour l'instant aux translations.

Parmi toutes les images translatées du point p choisissons un point q tel qu'il n'y ait aucune autre image dans le segment pq ; p et q sont dits voisins. 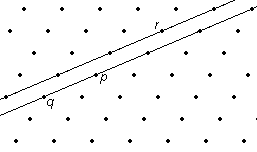Bien entendu comme il existe une translation qui amène p sur q , sur la droite pq on trouve toute une échelle de points transformés. Déplaçons la droite pq parallèlement à elle même jusqu'à ce que nous rencontrions un point r (peut-être plusieurs) ! Toutes les translations peuvent être obtenues en combinant la translation de vecteur pq et celle de vecteur pr . On obtient pour transformés de p tous les sommets d'un réseau de parallélogrammes et le groupe des translations est formés de toutes celles ayant pour vecteur px où x est un sommet quelconque du "parallélogrammage".

Il ne peut y avoir d'autres points; tout autre point serait sur le bord ou intérieur de l'un de ces parallélogrammes et cette situation contredirait: - soit l'hypothèse que p et q sont voisins, - soit qu'il n'y a pas d'autres points entre pq et la parallèle par r .

Des rotations ? Oui, mais lesquelles ?

A priori, on pourrait avoir des rotations dont l'angle est un multiple rationnel de 2 π . En fait on aurait chaque fois un groupe de rotations obtenu par répétition d'une rotation de π / n . Heureusement n n'est pas quelconque !

Nous allons, pour montrer cela, utiliser les transformées d'une rotation par les translations.

Supposons qu'il y ait une rotation de 2 π / n autour d'un point; il y a d'ailleurs tous les multiples de cette rotation. On dit que ce point est un centre de rotation d'ordre n .

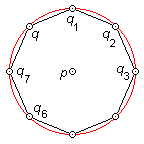
En transformant ce centre par les translations nous en trouvons une infinité d'autres. Mais peut-être y en a-t-il encore plus... De toutes manières, prenons deux centres d'ordre n à distance minimum, soit p et q . Transformons les rotations autour de q par celles autour de p ; nous obtenons une série de centres de rotations d'ordre n : q ₁ , q ₂ ,..., q _n = q , disposés sur un n -gone régulier inscrit fans un cercle de centre p . La distance séparant deux centres consécutifs vaut le côté du n -gone.

Or si n > 6 le côté est supérieur au rayon. Cela contredit notre choix de départ où nous avions pris deux centres à distance minimale. Il ne peut donc y avoir de centre de rotation d'ordre supérieur à 6. Voila qui limite sérieusement les possibilités !

Mais il y a mieux.

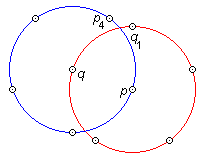Supposons qu'il existe des rotations d'ordre 5. Comme précédemment choisissons deux centres d'ordre 5, p et q , à distance minimum. En transformant par les rotations autour de p , nous obtenons 5 centres de rotations q i avec i allant de 1 à 5. Ici il n'y a plus de contradiction car le côté du pentagone est supérieur au rayon du cercle circonscrit. Mais...

Recommençons à transformer cette fois les rotations autour de p par celles autour de q et nous obtenons des nouveaux centres d'ordre 5 parmi lesquels p ₄ . Or p ₄ et q ₁ sont situés à une distance inférieure à pq , d'où, à nouveau, une contradiction.

En résumé, les seules rotations possibles correspondent à des centres d'ordre 2, 3, 4 ou 6.

Position des centres de rotations

Nous distinguerons 4 cas en considérant successivement les cas où les rotations sont au maximum d'ordre 2, 3, 4 ou 6.

1. uniquement des rotations d'ordre 2 (demis-tours, ou encore symétries centrales)

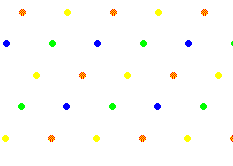
   Si nous partons de deux centres voisins par symétries successives nous obtenons une échelle de centres. En choisissant un des centres le plus proche de la droite qui supporte l'échelle, on construit tout le réseau des centres.

   Nous avons utilisé 4 couleurs différentes; tous les transformés d'un centre sont de même couleur; il y a 4 types de centres de rotation d'ordre 2.

2. au plus des rotations d'ordre 3

   A nouveau on part de deux centres de rotations d'ordre 3 voisins et on les transforme l'un par l'autre en répétant l'opération avec les nouvelles rotations obtenues. On complète en ajoutant les produits de ces rotations et on obtient une troisième famille de centres.

3. au plus des rotations d'ordre 4

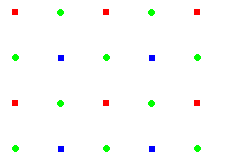
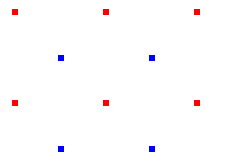   De même on part de deux centres d'ordre 4 à distance minimale. On ajoute tous les transformés successifs que l'on peut obtenir. Aucun autre centre d'ordre 4 ne peut exister sans qu'il contredise l'hypothèse de minimalité.

   Nous avons ajouté les centres d'ordre 2 que le groupe comporte.

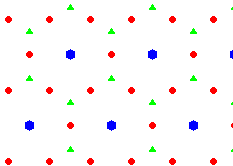
4. au plus des rotations d'ordre 6 En procédant de manière analogue on obtient tous les centres de rotations d'ordre 6 disposés aux sommets d'un découpage en triangles équilatéraux. Nous ajoutons les centres d'ordre 2 et 3 qui font partie du groupe.

En résumé si on se borne aux groupes cristallographiques ne contenant que des déplacements (et pas d'antidéplacement), on obtient 5 groupes notés p1, p2, p3, p4, p6 qui contiennent tous bien entendu des translations. De plus le groupe pi contient également des rotations d'ordre maximum i.

Et si on ajoute les antidéplacements ?

Les antidéplacements sont, soit des symétries glissées, soit des symétries axiales. Ils doivent évidemment conserver l'ensemble des centres de rotations ce qui limite très fortement la position de leurs axes. Une étude cas par cas, facile mais fastidieuse, donne:

• pour le groupe p1, on peut ajouter des symétries (glissées ou non) dans une seule direction (autrement la composée de deux symétries d'axes non parallèles donnerait une rotation). On obtient des groupes notés pm, pg, cm
• pour le groupe p2, les axes des symétries ou symétries glissées doivent être situés dans deux directions perpendiculaires. On obtient les groupes notés pgg, pmm, pmg, cmm
• en partant du groupe p3, les conditions sont plus fortes et on n'obtient que deux groupes notés p3m1 et p31m
• le groupe p4 livre également deux groupes notés p4m et p4g
• enfin p6 ne donne qu'un seul groupe noté p6m

En totalisant on a obtenu 12 groupes cristallographiques contenant des antidéplacements. Il existe donc au total 17 groupes cristallographiques .

Ce résultat date de la fin du XIX ^e siècle; les notations, bien que curieuses, sont standard et adoptées par tous les cristallographes.

Signalons que le problème réel (classification des groupes cristallographiques de l'espace à 3 dimensions) a été résolu à la même époque et donne lieu à 232 groupes !

Pour bien visualiser les choses, nous donnons un tableau montrant les 17 groupes opérant sur une figure ne possédant aucune symétrie (nous avons choisi la lettre F, initiale de figure).