1. Système de coordonnées cartésiennes - Repère cartésien
2. Coordonnées d'un point du plan - Coordonnées d'un vecteur.
3. Point partageant un vecteur dans un rapport donné - Rapport de section.
4. Equations d'une droite - Condition d'alignement de 3 points.
5. Birapport de 4 points alignés - Relations d'harmonie.
6. Nombres directeurs - Coefficient directeur d'une droite.
7. Droites parallèles.
8. Droites sécantes.
9. Faisceaux de droites - Equation d'un faisceau.
10. Condition nécessaire et suffisante pour que 3 droites appartiennent à un même faisceau.
11. Régions d'une droite - Signe d'une fonction linéaire.
12. Translation du repère - Translation du plan.
13. Changement de base - Affinité centrée ou application linéaire.
14. Changement de base - Affinité.

---

Une remarque préliminaire. Nous avons mis le terme analytique entre guillemets car l'analyse n'est jamais utilisée si ce n'est dans la section 11. Tout le reste ne relève que de l'algèbre ; hélas l'expression géométrie algébrique est déjà utilisée dans une autre domaine...

1. Système de coordonnées cartésiennes - Repère cartésien

Un système de coordonnées cartésiennes est déterminé par la donnée de deux droites sécantes en \(O\) (origine des coordonnées) et des points unités \(u, v\) sur chacune de ces deux droites.

Les vecteurs de base \(Ou\) et \(Ov\) seront désignés respectivement par \(\imath,\jmath \). Ces deux vecteurs, non proportionnels, doivent être linéairement indépendants).

Rappelons que la condition nécessaire et suffisante pour que deux vecteurs \(\imath \) et \(\jmath \) soient linéairement indépendants est : \( \lambda \imath + \mu \jmath = 0 \iff \lambda = \mu = 0 \).

Les supports des vecteurs \(Ou = \imath \) et \(Ov = \jmath \) sont appelés axes coordonnés (axe \(x'Ox\), axe \(y'Oy\)).

Remarque : Pour l'étude de propriétés affines (linéaires), les deux vecteurs de base sont arbitraires. Par contre, pour l'étude de propriétés métriques, nous verrons plus tard qu'il est plus commode de choisir deux vecteurs perpendiculaires de même module.

2. Coordonnées d'un point du plan - Coordonnées d'un vecteur.

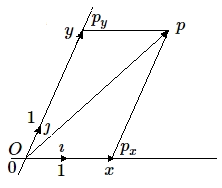
Etant donné un point \(p\), soient \(p_x\) et \(p_y\) ses 2 projections sur les axes coordonnés \(x'Ox\) et \(y'Oy\), parallèlement aux axes \(y'Oy\) et \(x'Ox\). Les deux vecteurs \(Op_x\) et \(Op_y\) sont les composantes du vecteur \(Op\) selon les axes coordonnés et \(Op = Op_x + Op_y\).

Chacune des composantes du vecteur OA peut être mesurée avec les vecteurs unités correspondants : \( x = Op_x/\imath ~~~~\text{et}~~~~ y = Op_y/\jmath\).

Les deux nombres (\(x,y\)) sont appelés coordonnées du point \(p\) dans le repère (\(\imath, \jmath \));

\(Op = x \imath + y \jmath \)

Cette décomposition est unique ! En effet, si \(Op = x \imath + y \jmath \) et \(Op = x' \imath + y' \jmath\), il en résulte que \(0 = (x - x') \imath+ (y - y') \jmath\). Or \(\imath\) et \(\jmath\) sont linéairement indépendants; il en résulte que x - x' = y - y'= 0 et par conséquent x = x' et y = y'

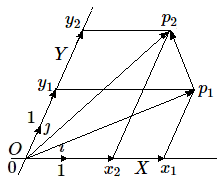
Etant donné le vecteur \(p_1p_2\), soient (\(x_1, y_1\)) et (\(x_2, y_2\)) les coordonnées de \(p_1\) et de \(p_2\). On a : \(p_1p_2 = Op_2 - Op_1\) Exprimons cette relation en fonction des vecteurs de base, il vient: \(p_1p_2 = (x_2 i + y_2 j) - (x_1 i + y_1 j) = (x_2 - x_1) i + (y_2 - y_1) j\)

En posant: \(p_1p_2 = X i + Y j\), on obtient : \[ X = x_2 - x_1 ~~~~\text{et}~~~~ Y = y_2 - y_1 \]

Les deux nombres \((X, Y)\) sont les coordonnées du vecteur \(p_1p_2\) dans le repère \((\imath, \jmath)\).Notons que sur le schéma ci-dessus, \(X = x_2-x_1\) est négatif.

Remarque : Les deux nombres \((X, Y)\) ne définissent pas le vecteur lié \(p_1p_2\) mais l'ensemble des vecteurs qui lui sont équipollents (vecteur libre).

Deux vecteurs sont équipollents si et seulement si leurs coordonnées sont égales

Deux vecteurs (\(X_1,Y_1\)) et (\(X_2,Y_2\)) sont parallèles \(\iff \begin{vmatrix}X_1 & Y_1 \\ X_2 & Y_2 \end{vmatrix} = 0\).

3. Coordonnées d'un point partageant un vecteur dans un rapport donné - Valeur du rapport de section d'un point sur un vecteur.

Soient les deux points \(p_1(x_1,y_1)\) et \(p_2(x_2,y_2)\). Considérons le point \(m(x_0,y_0)\) dont le rapport de section sur le vecteur \(p_1p_2\) vaut \(k\). On a \(k = mp_1/mp_2\) d'où \(mp_1 = kmp_2\) ; on en déduit : \(Op_1 - Om = k(Om_2 - Om)\) ou encore \((1-k)Om = Op_1 - k.Op_2\) On obtient finalement : \(Om = (Op_1 - k.Op_2)/(1 - k)\)

En exprimant cette relation en fonction des vecteurs de base: \(x_0 \imath + y_0 \jmath = [(x_1 i+ y_1 \jmath ) - k(x_2 \imath + y_2 \jmath )]/(1-k) = [(x_1-kx_2) \imath + (y_1-ky_2) \jmath ]/(1-k)\) On en déduit les coordonnées du point M :

\( \begin {cases} x_0 = (x_1 - kx_2)/(1-k)\\ y_0 = (y_1 - ky_2)/(1-k) \end{cases} \)

et la valeur de k :

\[ k = \normalsize{\frac{x_1 - x_0}{x_2 - x_0}} = \normalsize{\frac{y_1 - y_0}{y_2 - y_0}} \]

4. Equations d'une droite (paramétriques et statiques) - Condition d'alignement de 3 points.

4.1. Droite passant par 2 points

Etant donnés les points \(p_1, p_2\), si le rapport \(k = mp_1/mp_2\) varie, le point \(m\) décrit la droite passant par \(p_1\) et \(p_2\). Les coordonnées \((x, y)\) d'un point quelconque de la droite \(p_1 p_2\) sont:

\[ \begin{cases} x = \Large{\frac{x_1-kx_2}{1-k}}\\ \\ y = \Large{ \frac{y_1-ky_2}{1-k}}\end{cases} \]

Ces relations sont appelées équations paramétriques de la droite.

A chaque valeur de \(k\), y compris \(\infty\) correspond un point de la droite et réciproquement. En particulier à \(k=0\), correspond \(p_1\), à \(k = \infty\) correspond \(p_2\) et à \(k=1\) correspond le point à l'infini. En éliminant le paramètre k entre ces deux équations, on obtient la relation: \(x (y_1 - y_2) - y (x_1 - x_2) + x_1 y_2 - x_2 y_1 = 0\), qui peut s'écrire:

\( \begin{vmatrix}x & y & 1 \\x_1 & y_1 & 1 \\ x_2 & y_2 & 1\end{vmatrix} = 0 \)

Cette relation est l' équation statique de la droite passant par \(p_1\) et \(p_2\). On en déduit la condition nécessaire et suffisante d'alignement de 3 points \(p_0, p_1, p_2\) :

\(\begin{vmatrix}x_0 & y_0 & 1 \\x_1 & y_1 & 1 \\ x_2 & y_2 & 1\end{vmatrix} = 0 \iff p_0, p_1, p_2\) sont alignés.

4.2. Droite définie par un point et sa direction

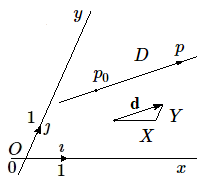
Soit un vecteur d \((X, Y)\). Considérons un point \(p_0(x_0, y_0)\) et recherchons l'équation de la droite D passant par \(p_0\) ayant la direction du vecteur d . \(p \in\) D \(\iff p_0p = k\) d \(\iff Op - Op_0 = k\) d \(\iff Op = Op_0 + k\) d

En fonction des vecteurs de base, on a : \( x\imath + y\jmath = x_0\imath + y_0\jmath+ k (X\imath+ Y\jmath)\), d'où:

\( \begin{cases} x = x_0 + kX \\ y = y_0+kY \end{cases} \)

Ce sont les équations paramétriques de la droite d passant par \(p_0(x_0, y_0)\) parallèle au vecteur de coordonnées \((X, Y)\). En éliminant le paramètre, on trouve pour la droite d l' équation statique :

\( \begin{vmatrix}x & y & 1 \\x_0 & y_0 & 1 \\ X & Y & 0\end{vmatrix} = 0 \)

Ce résultat correspond à associer à toute direction un point à l'infini (voir les coordonnées homogènes )

4.3. Toute relation linéaire entre \(x\) et \(y\) est l'équation d'une droite .

Dans les deux cas précédents, l'équation de la droite est de la forme \(ux + vy + w = 0\). Nous allons montrer que réciproquement \(ux + vy + w = 0\) est l'équation d'une droite (pour autant que \(u\) et \(v\) ne soient pas simultanément nuls). Remarque importante: Les coefficients \(u, v, w\) sont donnés à un facteur (non nul) près puisqu'il s'agit d'une équation.

Soit \(u_0x + v_0y + w_0 = 0\) une relation linéaire entre \(x\) et \(y\) où \(u_0, v_0, w_0\) représentent trois nombres donnés. Comme \(u_0\) et \(v_0\) ne sont pas simultanément nuls, il existe une infinité de couples \((x, y)\) vérifiant cette relation. Soient \(p_1(x_1, y_1),~~ p_2(x_2, y_2),~~ p_3(x_3, y_3)\) trois points distincts dont les coordonnées satisfont à la relation \(u_0x + v_0y + w_0 = 0\); on a donc:

\[ \begin{cases} u_0x_1+v_0y_1+w_0 = 0 \\ u_0x_2+v_0y_2+w_0 = 0 \\ u_0x_3+v_0y_3+w_0 = 0 \end{cases}\]

Si nous considérons ces trois relations comme provenant d'un système de 3 équations homogènes à 3 inconnues: \(u, v, w\), elles expriment que ce système possède une solution \(u_0, v_0, w_0\) non nulle. Il en résulte que son déterminant est nul; on a :

\[ \begin{vmatrix} x_1 & y_1 & 1 \\ x_2 & y_2 & 1\\x_3 & y_3 & 1 \end{vmatrix} = 0 \]

Or cette relation exprime que les trois points \(p_1,~~ p_2,~~ p_3\) sont alignés. Trois points quelconques de l'ensemble correspondant à \(u_0x + v_0y + w_0 = 0\) sont donc alignés; cet ensemble est donc une droite et toute relation de la forme \(ux + vy + w = 0\) est l'équation d'une droite.

Autre démonstration : Considérer un point \(p_0(x_0, y_0)\) de l'ensemble défini par \(ux + vy + w = 0\) ; étant donné un second point \(p(x,y)\) de l'ensemble, calculer les coordonnées du vecteur \(p_0p\). Montrer que ce vecteur est parallèle au vecteur fixe \(d\) (v,-u). En conclure que \(ux + vy + w = 0\) représente une droite et cette droite est parallèle au vecteur \(d(v,-u)\).

4.4. Autre forme de l'équation d'une droite.

Si une droite est définie par ses points d'intersection avec les axes coordonnés \(p(a,0)\) et \(q(0,b)\), elle a pour équation :

\[ \normalsize{\frac{x}{a}} + \normalsize{\frac{y}{b}} = 1 \]

Les nombres \(a,~b\) sont appelés respectivement abscisse et ordonnée à l'origine.

5. Birapport de 4 points alignés - Relations d'harmonie.

Soient \(p_1(x_1, y_1),~p_2(x_2, y_2),~p_3(x_3, y_3),~p_4(x_4, y_4)\), quatre points alignés.

Leur birapport \((p_1~p_2~p_3~p_4)\) est égal au rapport des rapports de section : \((p_3~p_1/p_3~p_2)/(p_4~p_1/p_4~p_2)\) Exprimons les rapports de section en fonction des coordonnées: \[ \begin{align} (p_1~p_2~p_3~p_4)& = [(x_1-x_3)/(x_2-x_3)]/[(x_1-x_4)/(x_2-x_4)]\\& = [(y_1-y_3)/(y_2-y_3)]/[(y_1-y_4)/(y_2-y_4)]\end{align} \]

On constate que :

\((p_1~p_2~p_3~p_4) = (x_1~x_2~x_3~x_4) = (y_1~y_2~y_3~y_4)\)

Si les 4 points sont sur la droite d'équations paramétriques: \[ \begin{cases} x = (x_1-kx_2)/(1-k)\\ y = (y_1-ky_2)/(1-k)\end{cases} \]

ou sur la droite d'équations paramétriques:

\( \begin{align} x =& x_0 + kX \\ y =& y_0+kY \end{align} \)

et correspondent aux valeurs \(k_1, k_2, k_3, k_4\) du paramètre \(k\) :

\((p_1~p_2~p_3~p_4) = (k_1~k_2~k_3~k_4) \)

Relation d'harmonie

Si le quaterne \(p_1~p_2~p_3~p_4\) est harmonique, c'est-à-dire si le birapport vaut -1 et que \(k_1,~k_2,~k_3,~k_4\) sont les 4 nombres correspondant aux 4 points, rappelons que:

\[ (k_1~k_2~k_3~k_4) = -1 \iff (k_1+ k_2)(k_3 + k_4) = 2(k_1.k_2 + k_3.k_4) \]

Cas particulier: si \(k_4 = 0\), on a: \(2/k_3 = 1/k_1 + 1/k_2\) et d'autre part, si \(k_3 + k_4 = 0\), on a: \(k_1.k_2 = k_3^2 = k_4^2\)

6. Nombres directeurs - Coefficient directeur d'une droite.

Les coordonnées d'un vecteur parallèle à une droite donnée sont appelées nombres directeurs de la droite; ces 2 nombres sont par conséquent donnés à un facteur près. Nous avons vu (4.4) que la droite \(ux + vy + w = 0\) est parallèle au vecteur d \((v, -u)\) ; par conséquent les nombres directeurs de \(ux + vy + w = 0\) sont proportionnels à \((v, -u)\) Remarque: Les nombres directeurs sont donnés à un facteur près.

Le rapport \(m = Y/X\) des nombres directeurs est appelé coefficient directeur de la droite. Si la droite est donnée sous la forme \(ux + vy + w = 0\), son coefficient directeur est:

\( m = -\Large{\frac{u}{v}} \)

Dans le cas d'une droite définie par les 2 points \(A_1(x_1, y_1)\) et \(A_2(x_2, y_2)\), on vérifiera que les nombres directeurs sont proportionnels à \((x_2 - x_1, y_2 - y_1)\), et que son coefficient directeur est:

\( m = -\Large{\frac{y_2 - y_1}{x_2 - x_1}} \)

Remarque: Le coefficient directeur est le coefficient de \(x\) lorsqu'on écrit l'équation de la droite sous la forme : \(y = mx + a\).

7. Droites parallèles

7.1. Condition nécessaire et suffisante de parallélisme de 2 droites:

Deux droites sont parallèles lorsque les vecteurs de ces droites sont parallèles et réciproquement.

\(\begin{cases}d_1\equiv u_1x+v_1y +w_1 \\ d_2\equiv u_2x+v_2y +w_2 \\ d_1\parallel d_2 \end{cases}\)

\(\iff\)

\(d_1(v_1,-u_1)\parallel d_2(v_2,-u_2)\)

\(\iff\)

\begin{align}& \begin{vmatrix}u_1 & v_1 \\u_2 & v_2\end{vmatrix} = 0\end{align}

est la condition nécessaire et suffisante de parallélisme de deux droites. Autrement dit, pour que 2 droites soient parallèles, il faut et il suffit que les coefficients des termes en x et en y dans leurs équations soient proportionnels.

7.2. Equation de la parallèle menée par un point à une droite.

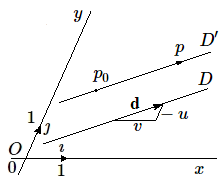
Etant donnés un point \(p_0(x_0, y_0)\) et une droite \(D \equiv ux + vy + w=o\), cherchons l'équation de \(D'\parallel D\) avec \(p_0 \in D'\). Nous savons que le vecteur d \((v, -u)\) est parallèle à D.

Soit \(p(x, y) \in D'\). Les coordonnées de \(p_0p\) sont \((x - x_0, y - y_0)\). Exprimons que \(p_0p \parallel D\) ; on obtient :

\(u (x - x_0) + v (y - y_0) = 0 \)

ce qui est l'équation de la droite D'.

8. Droites sécantes.

Soient les deux droites: \[ D_1\equiv u_1x + v_1y + w_1 = 0 \\D_2\equiv u_2x + v_2y + w_2 = 0 \]

Les coordonnées des points communs à \(D_1\) et \(D_2\) sont les solutions (si elles existent) du système formé par ces 2 équations.

Nous savons qu'il y aura une et une seule solution (un seul point) si :

\( \begin{vmatrix}u_1 & v_1\\u_2 & v_2 \end{vmatrix} \ne 0 \) c'est-à-dire si les droites ne sont pas parallèles.

Par contre si : \( \begin{vmatrix}u_1 & v_1\\u_2 & v_2 \end{vmatrix} = 0 \) , il y aura 0 ou une infinité de solutions

selon que les équations de \(D_1\) et de \(D_2\) ne sont pas ou sont proportionnelles, c'est-à-dire suivant que \(D_1\) et \(D_2\) sont distinctes ou non.

9. Faisceaux de droites - Equation d'un faisceau.

Soient deux droites distinctes :

\[ D_1\equiv u_1x + v_1y + w_1 = 0 \\D_2\equiv u_2x + v_2y + w_2 = 0 \]

Considérons la famille de droites: \(D \equiv \lambda (u_1x + v_1y + w_1) + \mu (u_2x + v_2y + w_2) = 0 \) ou encore \(D \equiv \lambda D_1 + \mu D_2 = 0\) avec \(\lambda\) et \(\mu \), deux nombres donnés à un facteur (non nul) près.

L'ensemble des droites D est appelé un faisceau de droites .

a) Si \(D_1\) et \(D_2\) sont sécantes en un point \(p\), ce point appartient à toutes les droites du faisceau. En effet, si \(p(x_0, y_0)\),

\[ p \in D_1 \implies u_1x + v_1y + w_1 = 0 \\ p \in D_2 \implies u_2x + v_2y + w_2 = 0 \]

Dans ce cas on obtient un faisceau de sécantes passant par le point P.

b) Si \(D_1 \parallel D_2\), on vérifie que les droites \(D\) sont parallèles, car elles ont les mêmes coefficients directeurs. Dans ce cas on obtient un faisceau de parallèles.

Montrons à présent que par tout point du plan \(m(x_1, y_1) \notin D_1 \cap D_2 \), il passe une et une seule droite du faisceau \(\lambda D_1 + \mu D_2 = 0 \) Pour cela calculons \(\lambda \) et \(\mu \). Il suffit d'exprimer que \(m \in D \); on obtient :

\[ \lambda (u_1x_1 + v_1y_1 + w_1) + \mu (u_2x_1 + v_2y_1 + w_2) = 0 \]

C'est une équation du premier degré en \(\lambda \) et \(\mu \) qui possède une infinité de solutions. Comme les coefficients de \(\lambda \) et de \(μ\) ne peuvent être simultanément nuls (\(m \notin D_1 \cap D_2 \)), la valeur du rapport \(\lambda /\mu \) est bien déterminée (éventuellement \(\infty \)).

10. Condition nécessaire et suffisante pour que 3 droites appartiennent à un même faisceau.

Soient \( D_1,~D_2,~D_3 \) , 3 droites distinctes.

a) Si \(D_3\) appartient au faisceau déterminé par \(D_1\) et \(D_2\), on a : \( D_3 \equiv u_3x + v_3y + w_3 \equiv \lambda (u_1x + v_1y + w_1) + \mu (u_2x + v_2y + w_2) = 0\) et le déterminant

\( E = \begin{vmatrix}u_1 & v_1 & w_1 \\u_2 & v_2 & w_2 \\ u_3 & v_3 & w_3 \end{vmatrix} = 0 \)

En effet le déterminant E, formé des coefficients des termes en x,y et des termes indépendants, est nul car la 3e ligne est combinaison linéaire des 2 premières.

b) Inversément; si on suppose que ce déterminant E soit nul ; il existe alors 3 nombres \(\alpha, \beta, \gamma \) non simultanément nuls, tels que :

\[ \begin{cases} \begin{align}\alpha u_1 + \beta u_2 ~+ \gamma u_3 = 0\\ \alpha v_1 ~+ \beta v_2 ~+ \gamma v_3 = 0\\ \alpha w_1 ~+ \beta w_2 + \gamma w_3 = 0\end{align} \end{cases} \]

Multiplions la première relation par \(x\), la seconde par \(y\), et la troisième par \(1\). En sommant il vient: \( \alpha D_1 + \beta D_2 + \gamma D_3 = 0 \)

Comme \(\alpha, \beta, \gamma \) ne sont pas simultanément nuls on peut supposer que \(\gamma \) n'est pas nul. On en déduit : \(D_3 = -(\alpha D_1 + \beta D_2)/\gamma \), ce qui exprime que la droite \(D_3\) appartient au faisceau déterminé par \(D_1\) et \(D_2\).

11. Régions d'une droite - Signe d'une fonction linéaire.

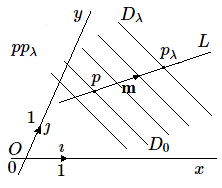Considérons la fonction: \(f(x, y) = ux + vy + w\) et étudions son signe pour les différents points du plan. \(f = 0\) sur la droite \(D_0\equiv ux + vy + w = 0\). Plus généralement, \(f\) prend une valeur constante \(k\), sur les droites \(D_\lambda \equiv ux + vy + w = \lambda \), c'est-à-dire sur les parallèles à \(D_0\).

Soient \(p(x_0, y_0) \in D_0\) et le vecteur m \((X, Y)\) non parallèle à \(D_0\). La droite \(L\) définie par \(p\) et m a pour équations:

\[ \begin{cases} x=x_0 + kX \\y= y_0 + kY \end {cases} \]

Cherchons les valeurs de \(k\) correspondant à \(p_\lambda = L \cap D_\lambda \)

\( u(x_0 + kX) + v(y_0 + kY) + w = \lambda \) ou encore \(ux_0 + vy_0 + w + k(uX + vY) = \lambda \). Mais \(p \in D_0 \equiv ux_0 + vy_0 + w = 0 \implies k = \lambda /(uX + vY) = \alpha\lambda \), où \(\alpha \) est une constante. Le vecteur \(pp_\lambda \) a pour coordonnées (\(α\lambda X, α\lambda Y\)) .

En posant n le vecteur de coordonnées (\(αX, αY\)) on a : \(pp_\lambda = \lambda \) n

À des valeurs de \(\lambda \) de même signe correspondront des points \(p_\lambda\) situés d'un même côté de \(p\) sur \(L\), et réciproquement. Comme la fonction est constante sur les droites \(D_\lambda \), on en déduit qu'elle garde le même signe dans chacun des demi-plans limités par \(D_0\).

Une droite détermine deux demi-plans. Une fonction linéaire détermine deux régions, l'une positive, l'autre négative, limitées par une droite.

Remarque: En pratique, étant donnée une fonction linéaire, on détermine le signe des régions en cherchant tout d'abord leur frontière D_0 et ensuite le signe de la fonction en un point du plan (origine, ou point sur un axe).

12. Translation du repère - Translation du plan.

a. Translation du repère.

Soit \(O'(x_0, y_0)\) l'origine d'un repère (\(\imath',\jmath'\)) équipollent au repère initial. Considérons un point \(p(x, y)\) et cherchons ses coordonnées (\(x', y'\)) dans le nouveau repère. On a:

\( \begin{cases} Op & = x\imath+ y\jmath \\ O'p & = x'\imath '+ y'\jmath'\end{cases}\)

D'autre part:

\(\begin{align} O'p & =  O'O + Op \\ & = - OO' + Op \\ & = - (x_0\imath + y_0\jmath) + x\imath + y\jmath \\ & =  (x - x_0)\imath + (y - y_0)\jmath \end{align}\)

d'où :

\[ \begin{cases} x' = x - x_0 \\y' = y - y_0 \end{cases} \]

b. Translation du plan.

Les équations ci-dessus peuvent également être envisagées sous un autre aspect. On suppose le repère fixe; \((x, y)\) sont les coordonnées d'un point \(p\) et \((x',y')\) les coordonnées d'un point \(p'\). Dans ce cas, le point \(p'\) se déduit du point \(p\) par la translation inverse de celle ci-dessus, de vecteur \((-x_0, -y_0)\).

13. Changement de base - Affinité centrée ou Application linéaire.

Considérons un nouveau repère \((\imath', \jmath')\) de même origine O.

Les vecteurs \(\imath'~\text{ et } ~ \jmath'\) ont pour valeur

avec \( \begin{vmatrix}a & b \\c & d \end{vmatrix} \ne 0 \) car les vecteurs \(\imath'\) et \(\jmath'\) ne sont pas proportionnels.

Soit \(p(x, y)\). Calculons les coordonnées \((x', y')\) de \(p\) dans la nouvelle base.

\( \begin{align} Op & = x\imath + y\jmath \\ & = x'\imath' + y'\jmath'\\& = x'(a\imath + b\jmath) + y'(c\imath + d\jmath) \\ & = (ax' + cy')\imath + (bx' + dy')\jmath \end{align}\)

d'où :

\(\begin{cases}x = ax' + cy'\\ y = bx' + dy'\end{cases}\)

avec

\(\begin{vmatrix}a & c \\b & d \end{vmatrix} \not = 0\)

A nouveau ces formules peuvent recevoir une autre interprétation. Lorsqu'on les considère comme liant les coordonnées \((x, y)\) d'un point \(p\), et les coordonnées \((x', y')\) d'un point \(p'\) dans le même repère, les points \(p\) et \(p'\) se correspondent dans une affinité centrée.

14. Changement de base - Affinité.

Le changement le plus général de repère s'obtiendra en combinant un changement de base avec un changement d'origine. Les équations seront donc:

\(\begin{cases} x = ax' + cy' + x_0 \\ y = bx' + dy' + y_0\end{cases}\)

avec

\(\begin{vmatrix}a & c \\b & d \end{vmatrix} \not = 0\)

Remarque : Dans la pratique les nombres \(a, b, c, d, x_0, y_0 \) sont déterminés en recherchant les nouvelles coordonnées de points particuliers (origine, points unités) ou en écrivant les équations des nouveaux axes coordonnés.

Si l'on considère un repère fixe, les équations ci-dessus lient les coordonnées \((x, y)\) d'un point \(p\) aux coordonnées \((x', y')\) d'un point \(p'\) transformé de \(p\) dans une affinité.

15. Aire d'un triangle

Soit un triangle dont les sommets \(p_1, p_2, p_3\) ont pour coordonnées: \((x_1, y_1), (x_2, y_2), (x_3, y_3)\) Nous utiliserons comme unité d'aire, le parallélogramme construit sur les vecteurs unités \(\imath = Ou, \jmath = Ov \) et \(Oe(= \imath + \jmath)\) De plus, nous supposerons le plan orienté de telle sorte que: Aire \(Ouev = +1\) et Aire \(Oveu = -1\).

Effectuons la translation amenant \(p_1\) à l'origine des coordonnées.

Le triangle \(O, p'_2(x_2 - x_1, y_2 - y_1), p'_3(x_3 - x_1, y_3 - y_1)\) a même aire que le triangle initial.

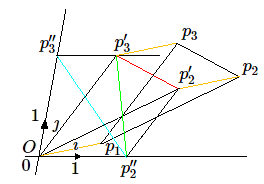
Par \(p'_2\) menons la droite p parallèle à \(Op'_3\).

Soit \({p''_2} = p \cap Ox\). Le triangle \(Op''_2p'_3\) est équivalent au triangle initial.

L'abscisse de \(p''_2\) a pour valeur: \([(x_2 - x_1)(y_3 - y_1) - (x_3 - x_1)(y_2 - y_1)]/(y_3 - y_1)\)

Par \(p'_3\) menons la parallèle à \(Op''_2 = Ox\). Le triangle \(Op''_2p''_3\) est équivalent au triangle \(Op''_2p'_3\) et par suite au triangle initial.

L'ordonnée de \(p''_3\) vaut \(y_3 - y_1\) ; l'aire du triangle vaut donc : \((Op''_2.Op''_3)/2\) \( = [(x_2 - x_1) (y_3 - y_1) - (x_3 - x_1) (y_2 - y_1)]/2\), ce qui peut s'écrire:

\[ \text{Aire } p_1p_2p_3 = 1/2 \begin{vmatrix}x_1 & y_1 & 1 \\x_2 & y_2 & 1\\x_3 & y_3 & 1 \end{vmatrix}\]

Remarque: En posant \(a = x_2 - x_1, b= y_2 - y_1, c = x_3 - x_1\) et \(d = y_3 - y_1\), par soustraction de la première ligne, le déterminant se ramène à \(\begin{vmatrix}a & b\\c & d \end{vmatrix}\). On obtient ainsi l'interprétation géométrique du déterminant 2 x 2. Sa valeur égale l'aire du parallélogramme construit sur les vecteurs \(Op'_2\) et \(Op'_3\). Cette interprétation est liée à l'application linéaire qui applique la base \((\imath, \jmath)\) sur la base \((Op'_2, Op'_3)\).