Introduction

Nous allons déterminer tous les pavages du plan associés à chacun des 17 groupes cristallographiques . Une classification en a été donnée à la fin des années 1960 par Heinrich Heesch, mais elle aboutissait à un nombre important de cas, certains pouvant être vus comme cas particuliers d'autres. Son travail a fait l'objet de simplifications dans un mémoire de Me Geneviève Dufey que j'ai dirigé en 1984. Nous sommes arrivés à associer pour 15 des 17 groupes un seul type de "pavé" et pour les deux groupes restants deux types, soit au total 19 types de "pavés".

Il n'entre pas dans nos intentions de donner tous les détails, parfois fastidieux, de la démonstration, mais plutôt d'en donner la ligne de conduite

Position du problème

Nous allons chercher les "pavés" qui permettent, sous l'action d'un groupe cristallographique, de recouvrir le plan. Les oeuvres de M.C.Escher nous montrent déjà qu'il y en a une infinité et le problème est d'y mettre un peu d'ordre.

D'une manière intuitive, on recherche la forme des pièces d'un puzzle dont toutes les pièces (supposées d'un seul tenant) sont identiques, et avec lesquelles on peut recouvrir la table (et même plus...) en respectant un des 17 groupes. Cette dernière condition est essentielle. En effet, si on n'en tient pas compte, on peut, par exemple, prendre des pièces carrées; on peut en faire des rangées et superposer celles-ci en en décalant de temps à autre l'une ou l'autre. C'est évidemment un recouvrement du plan, mais il n'est conservé par aucun des 17 groupes cristallographiques.

Remarquons que, tout comme les pièces d'un puzzle ne se superposent pas, les pavés ne peuvent pas se recouvrir; seule une partie de la frontière peut être commune. On en déduit que si on choisit un pavé P comme référence, tous les pavés sont en bijection (correspondance biunivoque) avec les éléments du groupe cristallographique.

Notation: à l'isométrie i , correspond le pavé P i = i ( P ) et inversement, à ce pavé, correspond l'unique isométrie i qui amène P sur P i .

Cas du groupe des translations p1

C'est le groupe le plus simple. Mais, étant donné sa simplicité, il ne fournit pas beaucoup de contraintes et ce cas est donc à la fois le plus simple et le plus compliqué !

Partons d'une pièce P . Il doit bien y en avoir une autre avec laquelle elle a une frontière commune. Puisqu'on recouvre tout le plan, par tout point de la frontière, il y a une autre pièce. Il se pourrait toutefois qu'elle n'ait en commun avec P que ce seul point, mais évidemment, ce cas ne peut survenir pour tous les points de la frontière. Nous ne détaillerons pas le raisonnement que nous laissons à ceux qui aiment ce genre de démonstrations. 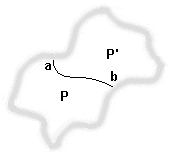Soit P' un pavé ayant avec P une frontière commune (nous laissons en flou le reste du contour qui n'est pas encore déterminé). A nouveau, il faut vérifier que la frontière est formée d'un seul arc ab (sinon les pièces ne seraient pas d'un seul tenant). 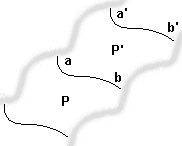Comme les seules isométries du groupe sont des translations, il existe une translation amenant P sur P' . Cette translation envoie l'arc ab sur l'arc a'b' . On obtient donc une nouvelle information sur la forme du pavé.

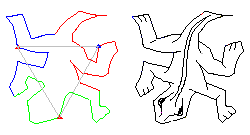
Répétons cette translation et son inverse en l'appliquant à P . Nous obtenons une "bande" infinie que vous pouvez voir ci-dessous.

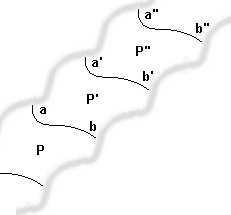
Voilà une partie du plan recouverte.

Nous allons utiliser les translations dans d'autres directions pour compléter le revêtement du plan. De nouveau, quand nous obtiendrons deux pièces adjacentes, la pièce comportera deux arcs translatés. Le bord gauche de cette bande ... a a' a" ... va s'appliquer sur le bord droit ... b b' b" ... 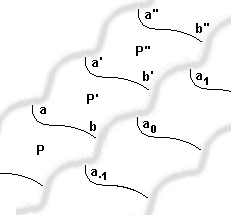Il serait "miraculeux" que les images des points ... a, a', a" ... coïncident avec les points ... b, b', b" ...

Désignons les images par ... a ₀ , a ₁ , a ₂ ... et corrigeons éventuellement la translation pour que le point a ₀ soit situé entre b et b' . Le translation inverse de celle utilisée amènera les points ... b, b',b" ... sur des points ... b ₀ , b ₁ , b ₂ .... Nous avons ainsi obtenu un recouvrement complet du plan par les pièces de notre puzzle qui seront toutes les translatées d'une pièce initiale (quelconque).

Mais à présent, nous disposons d'informations complètes sur la structure des frontières des pavés. 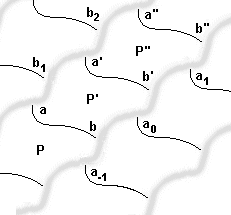L'arc ab ₁ est un translaté de a ₀ b'et l'arc b ₁ a'est un autre translaté de ba ₀ . Nous obtenons ainsi comme pavé (ou pièce de notre puzzle) une forme limitée par 6 arcs, deux arcs opposés étant translatés l'un de l'autre. 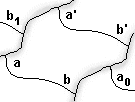La pièce obtenue est évidemment largement indéterminée, car nous sommes libres (dans certaines limites) de choisir la forme des arcs qui la limitent. En résumé on obtient tous les pavés pour le groupe p1 en partant d'un hexagone à côtés opposés parallèles et égaux. On fait alors subir à ses côtés rectilignes des déformations que l'on répercute à chaque fois sur les côtés opposés.

Nous dirons plus brièvement que:

Un pavé pour le groupe p1 est un "hexagone" dont les "côtés" opposés sont translatés. (Les guillemets sont là pour rappeler qu'il s'agit d'"hexagones" dont les "côtés" ne sont pas des segments, mais bien des arcs de courbes.)

Voici un exemple emprunté à l'artiste Maurits Cornelis Escher où l'on voit ce type de déformation. Après déformation, l'artiste décore l'intérieur de la pièce du puzzle de manière à faire apparaître une ou plusieurs figures (dans le cas un oiseau et un poisson) qui serviront à décorer le plan.

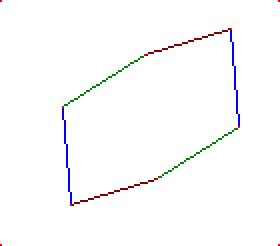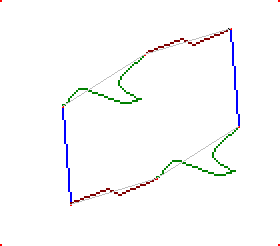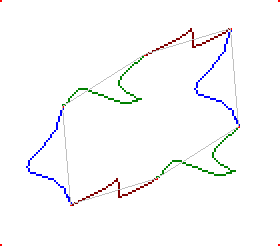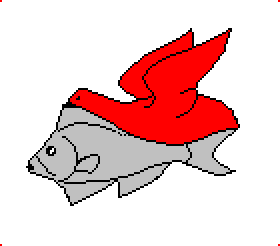
Notons que lorsque deux côtés opposés de l'hexagone sont nuls, l'hexagone se réduit à un parallélogramme. C'est malheureusement trop souvent le seul cas qui est décrit.

Il est d'ailleurs difficile de trouver dans l'œuvre de Escher des cas où le pavé dérive d'un hexagone et représente une seule figure. Par contre, dans le cas d'un pavé de type hexagonal, on trouve plusieurs exemples, mais le pavé représente deux, voire trois figures; il n'y a évidemment aucune contrainte sur la division et la décoration intérieure et le graphisme est ainsi rendu plus aisé.

Que se passe-t-il quand il y a des rotations ou des symétries axiales ?

Si l'on voit les choses de manière intuitive (un puzzle à pièces identiques) les pavés doivent s'emboîter et ne peuvent évidemment pas se chevaucher. Quand le groupe cristallographique possède des centres de rotations, ceux-ci ne peuvent être intérieurs aux pavés. Si un pavé contenait dans son intérieur un centre de rotation, un transformé par rotation autour de ce point donnerait un pavé qui le chevaucherait; donc le(s) centre(s) de rotation doivent être situés sur les bords des pavés. On peut faire le même raisonnement quand il y a des axes de symétrie. Là encore, pour une raison analogue, ils ne peuvent pas traverser les pavés mais doivent donc être situés en frontière de ceux-ci.

Un exemple: les pavages associés au p2

La remarque faite au sujet des éléments de symétrie nous indique que les centres de rotation d'ordre 2 sont situés sur la frontière du pavé.

Prenons un pavé P et construisons son symétrique P' par rapport à o , un des centres d'ordre 2 de sa frontière. Comme nous l'avons vu plus haut, si nous choisissons P comme pavé de référence, il correspond dans le groupe à l'identité et P' correspond à une symétrie centrale. Comme toutes les symétries centrales peuvent s'obtenir en composant l'une d'entre elles avec toutes les translations, nous en déduisons que la réunion des pavés P et P' donne un domaine qui est un pavé pour le sous-groupe des translations. Or, les domaines de p1 viennent d'être déterminés.

Nous en connaissons la forme: des "hexagones" à "côtés" opposés translatés. 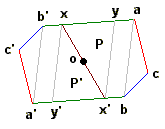Les "côtés" sont en fait des arcs de courbe, ce qui rend une visualisation un peu compliquée; nous conviendrons de dessiner simplement des segments de droite tout en conservant à l'esprit qu'il s'agit d'arcs de courbe. Examinons à présent les arcs qui limitent le domaine P : - l'arc xox' possède évidemment un centre de symétrie. - l'arc ac est translaté de c'a' mais c'a' a pour image dans la symétrie par rapport à o l'arc ca . Donc, en composant la translation avec la symétrie, on voit que ac est amené sur ca par une symétrie centrale et l'arc ac possède donc un centre de symétrie. - il en est évidemment de même pour l'arc bc . - reste l'arc xa que nous décomposons en les deux arcs xy et ya . Par un raisonnement identique à ceux qui précèdent, on voit que l'arc xy possède un centre de symétrie. Quant à l'arc ya , la seule information relative au pavé P est qu'il est translaté de x'b .

Nous pouvons résumer en disant que :

Un pavé pour le groupe p2 est un "hexagone" dont deux "côtés" opposés sont translatés et les 4 autres "côtés" possèdent un centre de symétrie. (N'oublions pas que "côté" est pris dans le sens "arc de courbe")

Pour les autres groupes contenant des centres de rotation ou des axes de symétrie, la méthode est la même; de plus, les contraintes dues au groupe deviennent de plus en plus fortes et rendent par conséquent la solution de plus en plus aisée. Nous nous bornerons à donner les résultats pour les groupes p3 , p4 et p6 et nous laissons comme exercice (simple) le cas où le groupe contient en plus des axes de symétries.

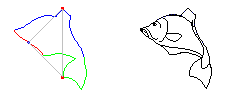
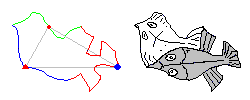
Pour le groupe p3 , le pavé est limité par un "hexagone" dont chacune des 3 paires de "côtés" consécutifs est formée d'un arc et de son transformé par une rotation d'1/3 de tour. Les 3 centres d'ordre 3 sont les sommets d'un triangle équilatéral. Le pavé correspondant au groupe p4 est constitué d'un "pentagone". Un des arcs possède un centre de symétrie et chacune des deux paires d'arcs consécutifs est formée d'un arc et de son transformé par 1/4 de tour. Enfin, pour le groupe p6 , le pavé est également un "pentagone". Un des arcs possède un centre de symétrie, la paire d'arcs consécutifs est formée d'un arc et de son transformé par une rotation d'1/3 de tour et la dernière paire d'arcs est formée d'un arc et de son transformé par une rotation d'1/6 de tour.

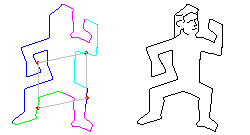
Nous montrons ci-dessous, pour chacun des groupes p2 , p3 , p4 et p6 , un exemple emprunté à Escher.

p2		p3

p4		p6

Attention, les couleurs n'interviennent qu'à titre artistique !

Le cas de symétries glissées

Restent les deux groupes pg et pgg qui contiennent des retournements (anti-déplacements) mais pas d'axe de symétrie.

Commençons par pg et partons d'un pavé P . Prenons un axe de symétrie glissée traversant P et considérons la réunion de P et son transformé P' par la symétrie glissée g d'amplitude minimale, de manière à ce que P et P' aient une portion de frontière commune xy .

Comme dans le cas du groupe p2 traité plus haut, nous obtenons un pavé pour le groupe des translations. Mais la différence essentielle avec le cas p2 réside dans le fait que ce pavé n'est pas invariant par la symétrie glissée g . Partant de P' , on peut construire P" , transformé de P' par g ; la réunion de P' et P" est également un pavé pour le groupe p1 . Ce pavé est tout simplement le transformé du premier par g .

Nous allons raisonner sur un dessin qui pourrait être complètement faux, (ne dit-on pas que la géométrie est également l'art de raisonner correctement sur des figures fausses ?), mais pour ne pas trop désorienter le lecteur, nous prendrons un dessin que nous savons être correct. Le pavé P 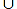P'est un "hexagone" abcdef avec ab || ed , bc || fe et cd || fa . Son transformé par g est P' 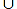P", un "hexagone" du même type. Intéressons-nous à la position de la frontière xy . Deux cas peuvent se présenter: xy coupe les "côtés" servant de frontière à deux "hexagones" consécutifs ou bien alors xy coupent deux "côtés" de l'hexagone ne faisant pas frontière.

Premier cas

Supposons que l'arc xy coupe les "côtés" faisant frontière entre les "hexagones".

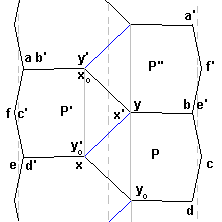
Désignons par y ₀ l'image de y dans la translation amenant ab sur ed et x ₀ l'image de x dans la translation inverse. De la sorte, on obtient une décomposition plus fine de l'"hexagone" en 10 arcs ax ₀ ybcd ₀ xef; la frontière de son transformé par g est également décomposée en 10 arcs (attention! il faut tourner en sens inverse puisque g change l'orientation) que l'on obtient en primant les lettres. En écrivant les relations existant entre les différents arcs qui bordent le pavé P , on voit que: - yb est le translaté de y ₀ d- bc est le translaté de fe = c'd' image de cd par g - xy = y' ₀ x'est l'image de y ₀ xpar g

Deuxième cas

Supposons que l'arc xy ne coupe pas les "côtés" faisant frontière entre les "hexagones"; supposons qu'il coupe cd et son parallèle af .

Notons x ₀ l'image de x dans la translation amenant cd sur af et y ₀ l'image de y dans la translation inverse. A nouveau, on considère la frontière de la réunion de P et P' , abcy ₀ xdefx ₀ y, et celle de la réunion de P' et P" où il suffit de prendre les mêmes lettres primées. En écrivant les relations existant entre les différents arcs qui bordent le pavé P on voit que: - xy est transformé par g en x'y' = ab , translaté de cd - yx ₀ est translaté de y ₀ x= f'e' qui est l'image de fe par g - x ₀ fest translaté de xd

On en tire le résultat suivant:

Un pavé pour le groupe pg possède une frontière formée de 6 arcs et est de l'un des deux types suivants:

• deux arcs se déduisant par translation sont encadrés par deux paires d'arcs se correspondant dans des symétries glissées, d'axes parallèles à la direction de la translation
• deux paires d'arcs se correspondant dans des symétries glissées sont encadrés par deux arcs se déduisant par une translation dans une direction perpendiculaire.

Pour le groupe pgg , on traite le cas de manière analogue, mais plus simple, puisqu'il existe des centres de symétrie.

On obtient le résultat suivant:

Un pavé pour le groupe pgg possède une frontière formée de 6 arcs et est de l'un des deux types suivants:

• deux arcs adjacents se correspondent dans une symétrie glissée; les deux adjacents sont translatés l'un de l'autre et les deux derniers arcs possèdent un centre de symétrie.
• deux arcs opposés se correspondent dans une symétrie glissée; deux arcs attenant à l'un d'eux sont transformés par une symétrie glissée d'axe perpendiculaire et les 2 arcs attenant à l'autre possèdent chacun un centre de symétrie.

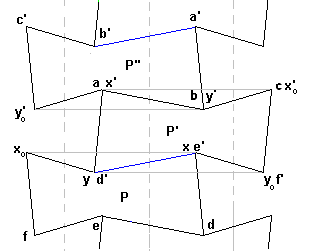
Nous donnons ci-dessous des exemples, pour pg empruntés à Escher.

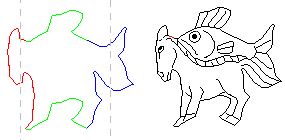
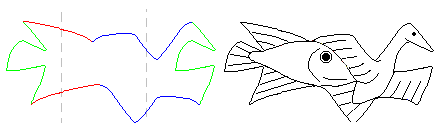
Pour le groupe pgg , nous n'avons pas trouvé d'exemples du cas général chez Escher. Heureusement, Dominique Ribault, mathématicien et artiste, graphiste et sculpteur, en a construits. Nous vous les présentons ci-dessous.

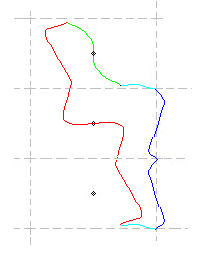
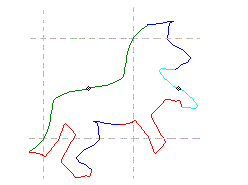
Et s'il y a des axes de symétrie ?

Nous ne décrirons pas ces cas; les résultats dérivent immédiatement de ce qui précède. La présence d'axes de symétrie permet de compléter le pavé par son symétrique et il suffit alors d'utiliser les résultats mentionnés plus haut. Dans ces cas, il y a évidemment plus de contraintes et la décoration devient plus "rigide"; à la limite, pour le groupe p6m , le pavé est un demi-triangle équilatéral !

Escher a fort peu utilisé ces groupes dont l'effet esthétique est bien moindre que les autres. Les figures ne vivent pas !

Un peu d'histoire

L'origine de ces décorations est due au fait que les religions sémites, notamment l'Islam, interdisent la représentation d'êtres vivants. Les artistes se sont alors tournés vers des motifs abstraits et le plus célèbre exemple est l'Alhambra de Grenade où l'on peut (paraît-il) retrouver des motifs utilisant les 17 groupes cristallographiques.

M.C.Escher l'a visité au cours d'un de ses nombreux voyages. Il a été très impressionné et a pris beaucoup de notes. A son retour, il a exploité sa découverte et développé de nouveaux motifs qui correspondaient mieux à sa personnalité. Escher n'était pas mathématicien, mais le hasard a fait que son épouse était compatriote et amie de la femme du grand mathématicien H.S.M.Coxeter. C'est par ce biais qu'Escher a reçu des compléments d'informations et vraisemblablement une orientation vers une généralisation de ses pavages à celui du plan hyperbolique .

A vous de jouer

Maintenant vous détenez la clé, ajoutez-y votre talent !