Chacun connaît le théorème relatif aux trois médianes d'un triangle : elles sont concourantes en un point appelé "centre de gravité" ! Est-il utile d'en rappeler sa démonstration ? Elle se base essentiellement sur le théorème de Thalès appliqué à un triangle. Plus précisément, sur le fait qu'un segment passant par les milieux de deux côtés est parallèle au troisième et en vaut la moitié.

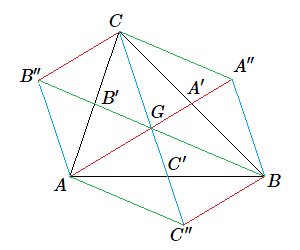Un simple examen de la figure ci-contre vous montrera de prouver d'une manière originale que les trois médianes du triangle \(A~B~C\) concourent en un même point \(G\). Soit \(A', B', C'\) les milieux des côtés du triangle \(A~B~C\). Partant des sommets \(A\) et \(B\), on construit les médianes \(A~A'\) et \(B~B'\) et on nomme \(G\) le point d'intersection. Grâce au théorème de Thalès, nous pouvons affirmer que la droite \(A'~B'\) est parallèle à la droite \(A~B\). Désignons par \(A''\) le point symétrique de \(G\) par rapport à \(A'\) et construisons de même les points \(B''\) et \(C''\). À nouveau, Thalès nous permet d'affirmer que \(A''B''\) est parallèle à \(A'~B'\). Le quadrilatère \(A~B~A''~B''\) est donc un parallélogramme centré en G. Comme les segments \(G~A'\) et \(A'~A''\) sont égaux, le point G est donc situé aux \(2/3\) de la médiane \(A~A'\). En utilisant les autres parallélogrammes de la figure, on en déduit finalement le théorème des médianes.

Par la suite, quand on a étudié le barycentre , il est aisé de calculer celui de 3 points \(A, B, C\) affectés chacun d'une masse identique. Il suffit de prendre le barycentre de deux d'entre eux, \(B\) et \(C\), par exemple, qui se trouvera en \(A'\), milieu du côté \(BC\). On termine en observant que le barycentre de \(A\) de masse \(1\) et de \(A'\) de masse \(2\) se trouve au \(2/3\) de la médiane \(A A'\).

Mais alors, le point \(G\) est le barycentre des 3 points de masse identique et le point \(G\) n'est peut-être pas le centre de gravité du triangle en tant que surface . Pensez à un triangle découpé dans une plaque de bois : on trouvera expérimentalement son centre de gravité en cherchant un point d'équilibre sur une pointe verticale. Mieux, on pourra le suspendre par divers points ; chaque verticale passant par le point donnera une indication sur la position du centre de gravité.

Mais alors comment trouver précisément le centre de gravité d'une surface triangulaire ?

La réponse était connue depuis bien longtemps, en particulier par Archimède ; comment procédait-il pour obtenir ce résultat ? Il se fait qu'à maintes reprises, Archimède utilise une démarche analogue à celle qui, par la suite, a donné naissance au calcul intégral ; il suffit de voir comment il applique (3 siècles av. JC.) le principe de Cavalieri (1598-1647) au calcul du volume de la sphère .

Pour trouver le centre de gravité d'un triangle, Archimède pose le triangle sur une base horizontale et le découpe en fines tranches horizontales ; chacune d'elles est un trapèze. Lorsque l'épaisseur des tranches diminue le trapèze devient de plus en plus proche d'un segment et son centre de gravité est donc le milieu de ce segment. Tous ces centres de gravité partiels sont donc situés sur la médiane du triangle. Comme cela reste vrai quel que soit le côté considéré comme horizontal, les trois médianes concourent au centre de gravité de la surface triangulaire.

Il faut noter que cette coïncidence (barycentre des sommets et centre de gravité de la surface) n'est plus vraie pour d'autres surfaces. En particulier, dans un trapèze isocèle, le barycentre des sommets (de masses identiques) est situé au milieu de la droite joignant les milieux des 2 bases parallèles. Si la largeur de la petite base se réduit petit à petit, le trapèze tend à devenir un triangle isocèle ; on voit ainsi que le centre de gravité n'est pas la limite du barycentre des 4 sommets.

En résumé, nous avons obtenu le centre de gravité des 3 sommets (par calcul du barycentre), celui de la surface triangulaire (méthode d'Archimède) mais quid du centre de gravité des 3 côtés du triangle ?

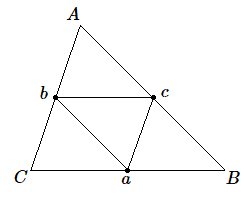Nous supposerons que les 3 barres, délimitant les côtés du triangle sont homogènes. Soit \(a, b, c\) la longueur des côtés \(BC, CA, AB\). Pour chacune des barres le centre de gravité se trouvera au milieu et il sera affecté d'une masse proportionnelle à \(a, b, c\). 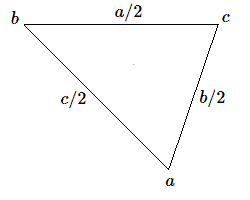On obtient donc la figure de gauche et on observe que les côtés du petit triangle médian sont de longueur \(a/2, b/2, c/2\). La masse affectée à un sommet est donc proportionnelle à la longueur du côté opposé.

Les centres de gravité partiels sont situés en des points partageant le côté opposé à un angle en segments proportionnels aux côtés adjacents. Mais c'est précisément une propriété des bissectrices d'un triangle !

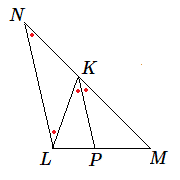Illustrons cela par un petit dessin. Soit le triangle \(KLM\) et la droite \(KP\) bissectrice de l'angle \(K\). Menons par le sommet \(L\) une parallèle à la bissectrice \(PK\) qui coupe le côté \(MK\) en \(N\). Les 2 angles égaux en K sont aussi égaux à ceux en \(L\) et \(M\). En projetant les points \(LPM\) parallèlement à la direction \(PK\) sur \(NKM\), on obtient: \[ \frac{LP}{PM} = \frac{NK}{KM}\] Comme le triangle \(LKN\) est isocèle de sommet \(K\), on a \(NK=LK\) ; il en résulte que : \[ \frac{LP}{PM} = \frac{LK}{KM}\]

Ce résultat nous permet de résoudre le problème posé plus haut. Pour obtenir les centres de gravité partiels, il suffit de tracer les bissectrices intérieures du triangle médian. Ces trois bissectrices concourent en un point qui, outre le fait d'être le centre du cercle inscrit dans le triangle, est le centre de gravité des 3 côtés du triangle.

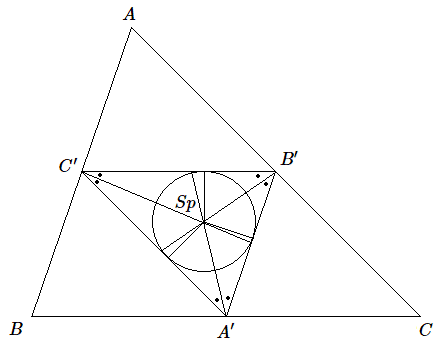
On obtient tout simplement le centre du cercle inscrit dans le triangle médian. Ce point est connu sous le nom de "point de Spieker" ; c'est le centre de gravité des côtés.

En résumé, un triangle possède plusieurs centres de gravité. Nous venons de déterminer celui des côtés ; celui des sommets est identique à celui du triangle-surface; c'est le point d'intersection des médianes.

Seul le calcul du barycentre de points massiques se généralise aisément.