Un kaléidoscope (du grec \(\kappa\alpha\lambda\omicron\varsigma \) = beau; \(\varepsilon\iota\delta\omicron\varsigma \) = forme; \(\sigma\kappa\omicron\pi\varepsilon\iota\nu \) = regarder) est un appareil formé de miroirs disposés de telle sorte que les réflexions multiples de petits objets colorés fassent apparaître de jolis motifs fort symétriques. D'un point de vue mathématique il s'agit de l'orbite d'un objet sous l'action du groupe engendré par les symétries planes des miroirs; nous allons dans ce qui suit étudier certains groupes engendrés par des symétries planes.

Tout d'abord quels sont les groupes engendrés par 2 symétries planes? Deux cas peuvent se présenter: les deux plans ont une droite en commun ou bien ils sont parallèles. Dans ce dernier cas le groupe engendré est un groupe de translations et symétries, l'amplitude de la translation minimale étant égale au double de la distance des deux plans. Dans le cas général où les deux plans sont sécants, le groupe engendré est un groupe de rotations et symétries; si l'angle des deux plans est \(\omega \), le produit des deux symétries planes est une rotation d'angle \(2\omega \). Le groupe contient donc toutes les rotations d'angle \(2m\omega \) où \(m\) est un entier. En général ce groupe sera infini; il sera fini s'il existe une valeur de \(m\) telle que \(2m\omega=2n\pi\). Dans ce cas on a un groupe fini de rotations et symétries d'ordre \(2k\) et on sait qu'alors l'angle minimum de deux plans de symétrie est \(\pi/k\). Ce groupe peut être engendré par les symétries par rapport à ces deux plans.

Passons à présent au cas de 3 plans de symétries. Ecartons deux cas: celui où les plans sont parallèles et celui où ils passent par une même droite.

Deux cas peuvent se présenter: les trois plans sont parallèles à une même direction (ils ont un point commun à l'infini) ou bien sont concourants en un point.

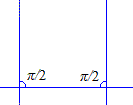
Si les trois plans passent par un même point on obtient un kaléidoscope sphérique . Etudions le cas où les trois plans sont parallèles à une direction D. Toutes les images de ces plans dans le groupe engendré sont parallèles à cette direction D et, par ce qui précède, on sait que l'angle minimum de deux plans sécants est \(\pi/k\), (\(k\gt 2\)). Si on sectionne par un plan perpendiculaire à D on obtient un pavage du plan par des triangles (à la limite ayant un sommet à l'infini) tous égaux et dont les angles valent \(\pi/k,\pi/l,\pi/m\) (éventuellement \(\pi/k,\pi/l,0\)). D'autre part, on sait que la somme des angles d'un triangle vaut \(\pi\). Le cas particulier se règle aisément: on obtient \(k=l=2\).

Passons au cas général; on a \(\pi/k+\pi/l+\pi/m=\pi\) ou

\[ \frac{1}{k}+\frac{1}{l}+\frac{1}{m}=1 \]

Supposons \(2\le k\le l\le m\). Cette équation diophantienne admet les solutions \((2,3,6)\), \((2,4,4)\) et \((3,3,3)\).

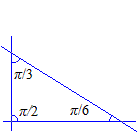
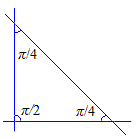
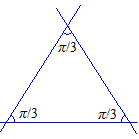
Afin de mieux nous représenter les choses et de pouvoir dessiner, regardons d'abord l'orbite (ensemble des images) d'un point sous l'action du groupe engendré par un kaléidoscope formé de 3 miroirs formant prisme, parallèles à une même direction D. On peut se ramener à un problème plan en considérant une section par un plan perpendiculaire à D. Soit dans un tel plan le triangle formé par les 3 miroirs et \(p\) un point intérieur. Cherchons l'orbite pour le groupe du kaléidoscope. Par produit des symétries par rapport aux 2 miroirs passant par un sommet et faisant un angle de \(\pi/n\), on obtient un polygone semi-régulier à 2n côtés.

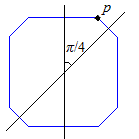
Nous avons deux manières d'imposer à ce polygone d'être régulier: ou bien nous plaçons le point \(p\) sur l'un des miroirs, et nous obtenons un n-gone régulier, ou bien nous plaçons \(p\) sur la bissectrice des deux miroirs et nous obtenons un 2n-gone régulier. Dès lors si l'on veut obtenir un pavage archimédien du plan (par polygones réguliers), associé à un groupe kaléidoscopique, on voit qu'il existe 7 possibilités pour le choix du point \(p\): en un des trois sommets du triangle, en un des trois pieds des bissectrices ou au point de concours des bissectrices. Nous indiquons pour chacune des positions admissibles de p le nombre de côtés des différents polygones du pavage.

Il est intéressant de réaliser les kaléidoscopes formés de trois miroirs parallèles à une même direction D et d'y montrer les pavages du plan que l'on peut obtenir à partir de ces derniers.

Bien entendu d'autres pavages par polygones réguliers sont possibles, et plus généralement il est intéressant d'étudier tous les pavages du plans homogènes en leurs "pavés", comme ceux utilisés par M.C.Escher .