Soient 3 miroirs, c'est-à-dire trois plans de symétrie concourant en un point O. Considérons les images de ces plans sous l'action du groupe engendré. Ils laissent invariantes les sphères de centre O.
Si les trois plans étaient parallèles à une même direction, les sphères auraient leur centre à l'infini et l'on aurait en fait un kaléidoscope plan . Les plans de symétrie et leurs images découpent sur une sphère de centre O un pavage par triangles. En effet, les angles des domaines découpés par les plans valent \(\pi/k\), \(k\ge 2\); ces domaines ne peuvent donc avoir plus de 3 côtés (p.ex. un quadrilatère sphérique ayant une somme des angles supérieure à \(2\pi\) aurait nécessairement un angle supérieur ou égal à \(\pi/2\)).
Les triangles sphériques ont une somme d'angles \(\gt \pi\); on a donc: \(\pi/k+\pi/l+\pi/m \gt \pi\),
\[ \frac{1}{k}+\frac{1}{l}+\frac{1}{m}\gt 1 \]Supposons \(2\le k\le l\le m\); on détermine facilement toutes les solutions: \((2, 2, m)\), \((2, 3, 3)\), \((2, 3, 4)\) et \((2, 3, 5)\). Dans le premier cas on a 2 plans, formant un angle de π / m , perpendiculaires à un troisième plan; le groupe est produit direct du groupe engendré par les symétries par rapport aux deux premiers plans (un groupe diédrique d'ordre \(2m\)) par le groupe engendré par la symétrie par rapport au troisième plan. On reconnaît pour les 3 autres groupes, le groupe des isométries du tétraèdre, celles du cube ou de l'octaèdre et enfin celles du dodécaèdre ou de l'icosaèdre.
Comment construire un tel kaléidoscope? Partons pour cela des polyèdres réguliers et calculons les angles \(\alpha, \beta, \gamma \) que font les arêtes du kaléidoscope correspondant. Les trois arêtes du kaléidoscope coupent le polyèdre au centre d'une face, au milieu d'une arête et en un sommet. Il est dès lors facile, en utilisant par exemple les coordonnées , de calculer ces angles; on trouve facilement les tangentes de ceux-ci.
Pour le tétraèdre: \(\mathbf{tan~}\alpha=2\sqrt{2}\), \(\mathbf{tan~}\beta=\mathbf{tan~}\gamma=\sqrt{2}\)
pour le cube: \(\mathbf{tan~}\alpha=\sqrt{2}\), \(\mathbf{tan~}\beta=1\), \(\mathbf{tan~}\gamma=\sqrt{2}/2\)
pour le dodécaèdre: \(\mathbf{tan~}\alpha=2\tau^2\), \(\mathbf{tan~}\beta=\tau \), \(\mathbf{tan~}\gamma=\tau^2\) avec \(\tau=\frac{\sqrt{5}-1}{2}\)
Remarquons que la somme des angles \(\alpha+\beta+\gamma \) vaut respectivement \(\pi,3\pi/4,\pi/2\) ; il suffit d'utiliser la formule:
\[ \mathbf{tan~}(\alpha+\beta+\gamma)=\frac{\mathbf{tan~}\alpha+\mathbf{tan~}\beta+\mathbf{tan~}\gamma-\mathbf{tan~}\alpha.\mathbf{tan~}\beta.\mathbf{tan~}\gamma} {1-\mathbf{tan~}\beta.\mathbf{tan~}\gamma-\mathbf{tan~}\gamma.\mathbf{tan~}\alpha-\mathbf{tan~}\alpha.\mathbf{tan~}\beta} \]En résumé, on a les valeurs approximatives suivantes pour les angles des arêtes des trois kaléidoscopes:
| \(\alpha \) | \(\beta \) | \(\gamma \) | |
| tétraèdre | 70°31'43" | 54°44'08" | 54°44'08" |
| cube-octaèdre | 54°44'08" | 45° | 35°12'52" |
| dodécaèdre-icosaèdre | 37°22'39" | 31°43'03" | 20°54'19" |
En développant les kaléidoscopes on obtient les figures suivantes :
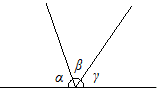
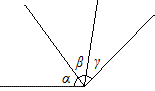

À partir de ces développements, il n'est guère difficile en utilisant trois miroirs de construire de tels modèles pour visualiser les symétries, les produits de symétries et les polyèdres archimédiens .
Si l'on fait choix d'un point \(p\), ses images engendrent un polyèdre ayant, en général trois types de faces semi-régulières, comme dans le cas du kaléidoscope plan . À nouveau, les positions de \(p\) dans un des trois miroirs ou dans l'un des trois plans bissecteurs rendent un des trois types de faces régulier, et par conséquent sept positions conduisent à des polyèdres à faces régulières .
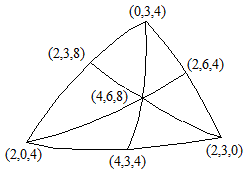
Indiquons schématiquement les positions des six plans dans le cas du groupe du cube. On peut voir les familles de polyèdres obtenus en se déplaçant dans chacune des six faces.
|
|
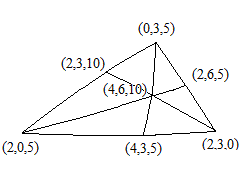
Indiquons schématiquement les positions des six plans dans le cas du groupe du dodécaèdre. On peut voir les familles de polyèdres obtenus en se déplaçant dans chacune des six faces.
|
|
Signalons enfin que les groupes kaléidoscopiques contiennent tous les groupes finis d'isométries. On a donc, outre les sous-groupes d'isométries (et de déplacements) des prismes et antiprismes, les trois groupes d'isométries des polyèdres réguliers, les trois groupes de déplacements correspondants, ainsi que le groupe formé des déplacements du cube conservant chacun des deux tétraèdres inscrits et des antidéplacements qui les permutent. Il est également intéressant de montrer les pavages de la sphère que l'on peut obtenir à partir de ces derniers.
Ces groupes kaléidoscopiques sont connus sous le nom de groupes de Weyl , du nom du mathématicien qui les étudia plus particulièrement.