Une généralisation possible des polyèdres réguliers conduit aux polyèdres archimédiens (du nom d' Archimède ) ou semi-réguliers. Une définition que l'on rencontre assez souvent est la suivante: ce sont des polyèdres convexes dont toutes les faces sont régulières de même que leurs sommets. Malheureusement cette définition n'est pas totalement satisfaisante car tous les polyèdres récoltés ont un groupe d'automorphismes transitif sur leurs sommets à une seule exception près! Il vaut mieux exiger, outre la régularité des faces, la transitivité du groupe d'isométries sur les sommets.

En dehors des prismes et antiprismes , on obtient 18 polyèdres dont les 5 polyèdres réguliers. Parmi les 13 polyèdres archimédiens proprement dits, il en est deux qui n'admettent aucun antidéplacement (il s'agit du "snub" cube et du "snub" dodécaèdre dont nous parlons par ailleurs); il reste donc 11 polyèdres semi-réguliers dont le groupe est un des groupes "classiques", c'est-à-dire celui du tétraèdre , du cube ou du dodécaèdre .

Ces groupes peuvent être engendrés par les symétries par rapport à 3 plans concourant en un point et formant un kaléidoscope sphérique . Comme le groupe est transitif sur les sommets du polyèdre ces sommets peuvent être obtenus comme éléments de l'orbite de l'un d'entre eux sous l'action du groupe.

On peut procéder par analogie avec le cas des pavages du plan (le plan étant assimilé à une sphère de rayon infini).

Pour obtenir des polyèdres semi-réguliers, le point dont on prend l'orbite devra se trouver soit dans le plan d'un miroir, soit dans le plan bissecteur de deux miroirs. Chacun des 3 groupes kaléidoscopiques ( tétraèdre, cube, dodécaèdre ) donne lieu à 7 polyèdres semi-réguliers (au sens large, y compris les réguliers).

Schématiquement on a:

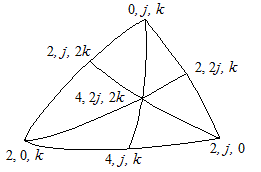
avec j, k = 3, 3 pour le groupe du tétraèdre, 3, 4 pour celui du cube et 3, 5 pour celui du dodécaèdre.

Etant donné le caractère symétrique du kaléidoscope associé au tétraèdre, nous pouvons éliminer deux polyèdres qui sont obtenus deux fois. D'autre part, on retrouve les 5 polyèdres réguliers aux sommets entourés d'un cercle. Restent donc 14 polyèdres archimédiens proprement dits. Or des listes (soigneusement faites!) n'en mentionnent que 11. Archimède a-t-il "oublié" 3 polyèdres ?

Pas vraiment!

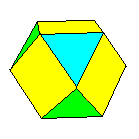
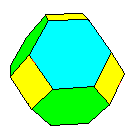
Les 3 polyèdres supplémentaires que nous récoltons ainsi sont dus au fait que le groupe du tétraèdre est un sous-groupe d'indice 2 de celui du cube. On obtient les polyèdres bicolores (c'est-à-dire où deux faces adjacentes ont deux couleurs différentes):

Les groupes d'automorphismes de ces polyèdres bicolores sont isomorphes à celui du tétraèdre; si l'on supprime les couleurs, leur groupe est celui du cube.

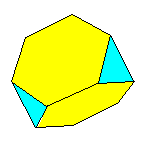
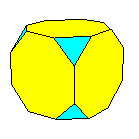
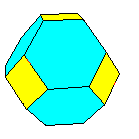
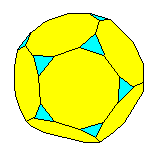
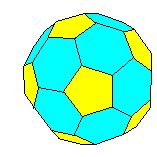
Un mot sur les dénominations: des polyèdres réguliers. On peut dériver certains polyèdres à partir des polyèdres réguliers en tronquant les sommets à une distance telle que les faces qui contenaient le sommet deviennent des polygones réguliers:

En tronquant un peu plus de telle manière que les faces par un sommet redeviennent des polygones réguliers, on obtient:

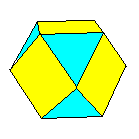
De plus en tronquant à nouveau les deux polyèdres ci-dessus :

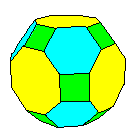
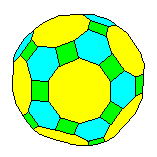
Pour l'anecdote, notons que rhombi vient du grec rombos signifiant losange; ces polyèdres ont des faces carrées mais chacun sait qu'un carré mis sur sa pointe devient un losange...!