Il existe 24 déplacements qui conservent un cube; on peut les énumérer: les rotations d'1/4 de tour, dans un sens ou dans l'autre: il y en a 6; les rotations de 2/4 de tour: il y en 3; les rotations d'1/3 de tour, dans un sens ou dans l'autre: il y en a 8, les rotations d'1/2 tour: il y en a 6, ce qui fait un total de 23 rotations auxquelles il convient d'ajouter l'identité. Total: 24.
Si nous choisissons un point de l'espace et que nous lui appliquons les 24 déplacements, nous obtiendrons, en général, un ensemble de 24 points, éventuellement moins (un diviseur de 24) si le point est mal choisi (par exemple sur un axe de rotation).
Cette figure qui comporte 24 sommets est fort régulière; en particulier elle contient des carrés (orbites sous l'action des rotations d'ordre 4) ainsi que des triangles équilatéraux (obtenus à partir des axes d'ordre 3). Ces carrés et ces triangles équilatéraux ne se touchent qu'en un sommet; le reste de la figure est formé de quadrilatères gauches comme on peut l'observer.
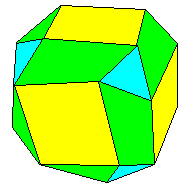
Examinons la figure en supposant (sans nuire à la généralité) que le point choisi est le point \((1,a,b)\) \(a\gt 0\) et \(b\gt 0\); il possède 24 transformés: on a par exemple dans le plan \(x=1\) les points \((1,a,b), (1,b,-a), (1,-a,-b)\) et \((1,-b,a)\); dans le plan \(y=1\) les points \((-a,1,b)\), \((b,1,a), (a,1,-b)\) et \((b,1,-a)\) etc. Nous disposons de 2 paramètres \(a\) et \(b\) pour essayer d'obtenir une figure encore plus régulière. En dehors des carrés et des triangles, cette figure contient des quadrilatères gauches admettant un axe d'ordre 2. Divisons chacun de ces quadrilatères en 2 triangles. Choisissons \(a\) et \(b\) de telle manière que ces triangles soient équilatéraux; dès lors les carrés et les triangles que nous avions déjà auront tous des côtés de même longueur. Algébriquement on est conduit aux équations suivantes:
\[ (a-b)^2+(b+a)^2=(b-1)^2+(1-a)^2+(a-b)^2 \] (côté du carré égal au côté du triangle), et \[ (a-b)^2+(b+a)^2=(1-a)^2+(a-1)^2+(2b)^2 \] (les triangles sont équilatéraux).Ces relations donnent:
\[ \begin{cases} ab+a+b-1=0 \\ \\ b^2-2a+1=0 \end{cases} \]d'où :
\[ a^3+a^2+a-1=0 \]Les solutions approchées valent \(a\approx 0,543684\) et \(b\approx 0,295598\).
Le polyèdre ainsi construit possède évidemment toutes les symétries du cube (mis à part les antidéplacements qui changent l'orientation). De plus il existe un et un seul déplacement amenant un sommet sur un sommet. Cette propriété permet d'identifier le snubcube au groupe du cube : il suffit d'en particulariser un sommet n et d'attribuer à tout autre sommet le nom de l'unique déplacement qui applique le sommet n sur le sommet choisi. Le produit d'un déplacement D par le déplacement D' est le déplacement D" correspondant au sommet image de D par le déplacement appliquant n sur D'.
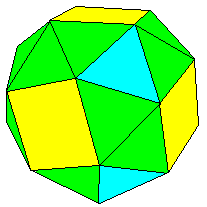
Le snubcube possède 6 faces carrées, 8 faces triangulaires (associées aux 8 sommets du cube) et 12 paires de faces triangulaires (associées aux 12 arêtes du cube). Le polyèdre s'appelle snubcube, ce que l'on peut traduire par cube "adouci" ou bien encore par cube "camus".
Si l'on part du groupe du dodécaèdre , en procédant de manière analogue on construit un polyèdre à 60 sommets (l'ordre du groupe des déplacements du dodécaèdre). Ce polyèdre possédera 12 faces pentagonales, 20 faces triangulaires.

Cette figure s'appelle le snubdodécaèdre (dodécaèdre adouci ou camus).
Si on procédait de même à partir d'un tétraèdre , on obtiendrait un snubtétraèdre. Or dans la littérature on n'en parle jamais ! Pourtant ce polyèdre existe évidemment. Il a 12 sommets (l'ordre du groupe des déplacements du tétraèdre). Il possède 4 faces triangulaires, 4 faces triangulaires (correspondant aux sommets) et 6 paires de faces triangulaires, soit un total de 20 faces triangulaires. Il s'agit en fait d'un icosaèdre (inscrit dans un tétraèdre).
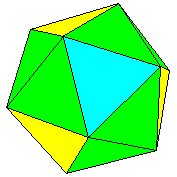
Inversement le tétraèdre est circonscrit à l'icosaèdre: il s'obtient en prolongeant 4 des 20 faces. On peut circonscrire 5 tels tétraèdres autour d'un icosaèdre. De même, de manière duale on peut inscrire 5 tétraèdres dans un dodécaèdre en utilisant chaque sommet une et une seule fois. Les 60 déplacements du groupe donnent les 60 permutations paires des 5 tétraèdres.
Nous vous conseillons vivement de jeter un coup d'œil sur l'article de la section " En 3 dimensions " qui vous permettra de vous familiariser avec tous les polyèdres rencontrés.