Nous avons étudié les kaléidoscopes formés par 3 miroirs.
Si les trois miroirs sont parallèles à une même direction, on peut se ramener au cas des kaléidoscopes plans . Dans le cas où les trois miroirs ont un point commun il s'agit des kaléidoscopes sphériques .
Les images d'un point quelconque donnent les sommets d'un pavage par polygones semi-réguliers. De manière plus précise si les angles des trois miroirs valent respectivement \(\pi/i, \pi/j, \pi/\), les polygones semi-réguliers auront respectivement \(2i, 2j\) et \(2k\) côtés.
Par choix d'un point particulier le polygone semi-régulier peut devenir régulier. Si, par exemple dans le cas où les deux miroirs font un angle de \(\pi/n\), l'on choisit un point situé dans un plan bissecteur de l'angle de deux miroirs, les deux types de côtés du polygone semi-régulier deviennent égaux et le polygone est un polygone régulier de \(2n\) côtés. Un autre choix consiste à placer le point dans un des miroirs. Dans ce cas une famille de côtés a une longueur nulle et le polygone devient régulier mais à n côtés seulement. Remarquons que si \(n = 2\) il s'agit d'un digone, c'est-à-dire un segment. Dans un cas extrême, le point est choisi sur l'intersection de deux miroirs, et alors tous les côtés du polygone ont une longueur nulle: le polygone est réduit à un point.
Nous retrouverons ainsi les polyèdres archimédiens symétriques
Considérons les différents kaléidoscopes sphériques.
Angles de \(\pi/2, \pi/3, \pi/3\)
En général, les polygones semi-réguliers auront respectivement \(4, 6\) et \(6\) côtés; ce nombre sera divisé par 2 si le point est situé dans un des miroirs; il sera égal à 0 s'il est à l'intersection de deux miroirs.
Nous représentons sur la figure les 7 positions donnant lieu à un pavage par polygones réguliers en y indiquant le nombre de côtés de chacun d'entre eux. Les polygones engendrés par réflexions autour du sommet supérieur sont dessinés en bleu, ceux autour du sommet inférieur gauche en vert et ceux autour du sommet inférieur droit en rouge.
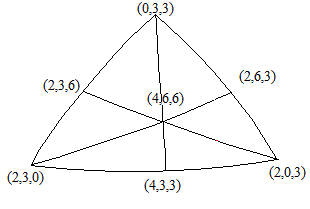
On obtient 7 types de pavage de la sphère correspondant aux polyèdres archimédiens de la famille du tétraèdre .
Angles de \(\pi/2, \pi/3, \pi/4\)
En général, les polygones semi-réguliers auront respectivement \(4, 6\) et \(8\) côtés; ce nombre sera divisé par 2 si le point est situé dans un des miroirs; il sera égal à 0 s'il est à l'intersection de deux miroirs.
Nous représentons sur la figure les 7 positions donnant lieu à un pavage par polygones réguliers en y indiquant le nombre de côtés de chacun d'entre eux. Les polygones engendrés par réflexions autour du sommet supérieur sont dessinés en bleu, ceux autour du sommet inférieur gauche en rouge et ceux autour du sommet inférieur droit en vert.
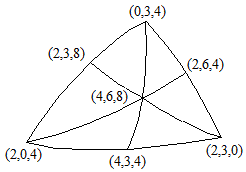
On obtient 7 types de pavage de la sphère correspondant aux polyèdres archimédiens de la famille du cube .
Angles de \(\pi/2, \pi/3, \pi/5\)
En général, les polygones semi-réguliers auront respectivement \(4, 6\) et \(10\) côtés; ce nombre sera divisé par 2 si le point est situé dans un des miroirs; il sera égal à 0 s'il est à l'intersection de deux miroirs.
Nous représentons sur la figure les 7 positions donnant lieu à un pavage par polygones réguliers en y indiquant le nombre de côtés de chacun d'entre eux. Les polygones engendrés par réflexions autour du sommet supérieur sont dessinés en bleu, ceux autour du sommet inférieur gauche en vert et ceux autour du sommet inférieur droit en rouge.
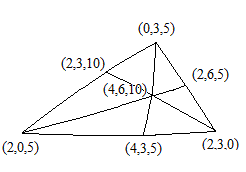
On obtient 7 types de pavage de la sphère correspondant aux polyèdres archimédiens de la famille du dodécaèdre .
Nous vous conseillons vivement de jeter un coup d'œil sur la section " En 3 dimensions " qui vous permettra de vous familiariser avec tous les polyèdres rencontrés.