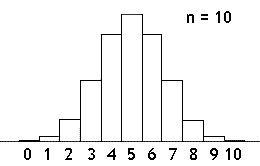Si un événement a une probabilité \(p\) de se produire, et par conséquent une probabilité \(q=1-p\) de ne pas se produire, on sait que la probabilité d'avoir \(k\) réussites au cours de \(n\) expériences est donnée par la loi :

\[ P_n(k) = {n\choose k} p^kq^{n-k} \]

appelée loi binomiale, car la somme des \(P_n(k)\) est le développement du binôme \((p+q)^n\):

\[ (p + q)^n = \sum_{k=0}^{n} P_n(k) = \sum_{k=0}^{n} {n\choose k} p^kq^{n-k} \]

Il n'est pas très difficile de calculer la moyenne et l'écart pour cette loi.

La moyenne est:

\[ { \mu = \sum_{k=0}^{n} k {n\choose k} p^kq^{n-k} = \sum_{k=1}^{n} {{n-1}\choose k} p^{k-1}q^{n-k} = np }\]

Le résultat est bien celui attendu; si l'on effectue \(n\) expériences et que chacune d'elles à une probabilité \(p\) de réussite on aura en moyenne \(np\) réussites. Bien entendu la probabilité d'avoir exactement \(np\) réussites est en général faible.

L'écart se calcule d'une manière assez semblable:

\[ \begin{aligned} \sigma^2& =\sum_{k=0}^{n} k^2 {n\choose k} p^kq^{n-k} - n^2p^2 \\ & = \sum_{k=1}^{n} k {{n-1}\choose {k-1}} p^{k-1}q^{n-k}np - n^2p^2 \\ & = (\sum_{k=1}^{n} k {{n-1}\choose {k-1}} p^{k-1}q^{n-k}-np).np \\ & = (\sum_{k=1}^{n}(k-1) {{n-1}\choose {k-1}} p^{k-1}q^{n-k} + \sum_{k=0}^{n-1} {{n-1}\choose {k-1}} p^{k-1}q^{n-k}-np).np \\ \\ & = (((n-1)p+1-np ).np) \\ \\ & = npq \end{aligned} \]

Dans le cas où la probabilité p est très faible, on peut approcher la distribution binomiale par une autre, appelée loi de Poisson .

Si on dessine l'histogramme d'une loi binomiale on obtient un graphique qui fait songer à la courbe en cloche, c'est-à-dire à la loi normale qui, elle, est continue. En fait, on s'en rapproche d'autant plus que le nombre n d'épreuves est grand.