Partons d'une distribution binomiale et faisons tendre le nombre \(n\) d'épreuves vers l'infini.

Si \(p\) est fixé au départ, la moyenne \(np\) tend également vers l'infini; de plus l'écart \(npq\) tend également vers l'infini. (Le cas où p varie et tend vers 0 tout en laissant fixe la moyenne m = np sera étudié par ailleurs et donnera lieu à la distribution de Poisson ).

Si on veut calculer la limite de la distribution binomiale, il s'agira donc de faire un changement d'origine qui stabilise la moyenne, en 0 par exemple, et un changement d'unité qui stabilise l'écart, à 1 par exemple.

Voyons tout d'abord comment varie \(P_n(k)\) en fonction de \(k\) et calculons la différence:

\[ \begin{align} P_n(k+1)-P_n(k)& ={n\choose{k+1}}p^{k+1}q^{n-k-1}-{n\choose{k}}p^kq^{n-k} \\ & ={n\choose{k}}p^ka^{n-k}\left[\frac{(n-k)p}{(k+1)q}-1\right] \\ & =P_n(k)\frac{np-k-q}{(k+1)q} \end{align} \]

On en conclut que \(P_n(k)\) est une fonction croissante de \(k\), tant que \(np-k-q\) est positif. Remarquons que \(q\lt 1\) et que par conséquent les deux valeurs de \(k\) voisines de la moyenne \(np\) constituent les maxima de \(P_n(k)\). D'autre part la différence \(P_n(k+1)-P_n(k)\) est le taux d'accroissement de la fonction \(P_n(k)\) ; il peut s'écrire sous la forme:

\[ \frac{\Delta P_n(k)}{\Delta k} = \frac{P_n(k+1)-P_n(k)}{(k+1)-k} \]

Si \(n\) devient grand, \(k\) l'est également, pour autant que \(p\) soit fixé et que l'on s'intéresse aux valeurs de la fonction proches de la moyenne; les variations de \(k\) deviennent négligeables par rapport à \(k\). Si l'on effectue un changement de variable adéquat, la variation de la nouvelle variable tend vers 0 et l'on est conduit à effectuer un passage à la limite. Remplaçons \(k\) par une nouvelle variable \(x\) dont la moyenne soit \(0\) et telle que son écart vaille \(1\); on a \(x=\Large \frac{k-np}{\sqrt{npq}}\) ; appelons \(F(x)\) l'expression de \(P_n(k)\) en fonction de la nouvelle variable. Le taux d'accroissement de \(F(x)\) vaut:

\[ \frac{\Delta F(x)}{\Delta x}=\frac{\Delta P_n(k)}{\Delta k}\frac{\Delta k}{\Delta x}=\frac{\Delta P_n(k)}{\Delta k}\sqrt{npq} \] et, en appliquant le résultat trouvé précédemment, on obtient: \[ \begin{align} \frac{\Delta F(x)}{\Delta x}& =\frac{-(k-np)-q}{(k+1)q}P_n(k)\sqrt{npq} \\ & =\frac{-[(k-np)+q]np}{\sqrt{npq}}P_n(k) \end{align} \]

Après un passage à la limite pour \(n\) tendant vers l'infini, tenant compte de ce que \(q\lt 1\) et du fait que les valeurs de \(k\) considérées se trouvent au voisinage de la moyenne \(np\), on obtient:

\[ \frac{dF(x)}{dx} = -xF(x) \]

Cette équation peut encore s'écrire: \(\frac{dF(x)}{F(x)} = -x.dx\) et en intégrant les deux membres de cette égalité on obtient \(\mathbf{ln~}F(x)=-\frac{x^2}{2}+K\). Les solutions sont les fonctions \(F(x)=\lambda e^-\frac{x^2}{2}\). La constante est déterminée par la condition que \(\int_{-\infty} ^{+\infty} F(x)dx\), qui représente la somme de toutes les probabilités, vaut 1. On peut montrer que \(\lambda=\large\frac{1}{\sqrt{2\pi}}\) et on obtient donc la loi de Gauss , dite loi normale.

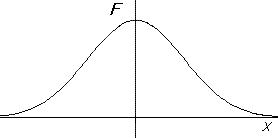\[ F(x)=\frac{1}{\sqrt{2\pi}}e^-\frac{x^2}{2} \]

En revenant aux variables non normées, on obtient:

\[ \large\frac{1}{\sigma \sqrt{2\pi}} e^{-\frac{1}{2} {(\frac{x-m}{\sigma})^2}} \]

Cette loi régit sous des conditions très générales, et souvent rencontrées, beaucoup de phénomènes aléatoires .

Ci-dessous, nous vous présentons la " Planche de Galton " qui visualise le lien entre une distribution binomiale avec p=q=1/2 et la loi normale.