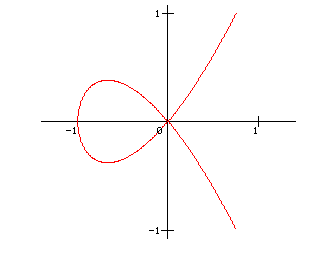Dans cet article, nous allons étudier quelques courbes du troisième degré. Cela nous changera du second degré !

La courbe de départ sera assez simple : une strophoïde ou plus exactement une courbe de la famille des strophoïdales. Cette courbe est décrite algébriquement par une équation du 3e degré d'équation \(x^3+x^2-y^2\). Nous l'avons déjà rencontrée à plusieurs reprises : à l'occasion des études de fonctions ainsi que dans l'article consacré aux coordonnées polaires .

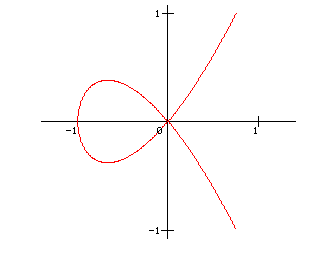
Généralement, les cubiques ne sont pas des courbes rationnelles à moins que, comme dans le cas de la strophoïde, elles possèdent un point double c'est-à-dire un point tel que toute droite passant par ce point possède deux intersections confondues.

Dans ce cas, dans le faisceau des droites passant par le point double, chacune des droites la coupe, puisque c'est une cubique selon 3 points : 2 des points sont confondus en le point double et le troisième point d'intersection varie (quitte à partir à l'infini !). Par conséquent, les coordonnées des points de la cubique peuvent s'exprimer en fonction rationnelle d'un paramètre. Dans le cas présent, les abscisses de l'intersection d'une droite \(y=tx\) passant par le point double sont données par l'équation du 3e degré \(x^3+x^2-t^2 x^2=0\). Elle se factorise \(x^2(x+1-t^2)=0\) et donne une solution double (\(x=0\)) correspondant au point double et une troisième solution \(x=t^2-1\).

Cette cubique peut donc être décrite par les équations paramétriques:

\[ \begin{cases}x=t^2-1\\y=t^3-t\end{cases} \]

Lorsqu'il n'y a pas de point double, la cubique n'est plus une courbe rationnelle et ses équations paramétriques font appel à d'autres fonctions (dites elliptiques).

L'étude de ces courbes est plus compliquée. Néanmoins, il est intéressant de voir l'allure de ces courbes. Partons du graphique de la strophoïde et "cassons" son point double ; pour ce faire, considérons les courbes d'équation \(x^3+x^2-y^2=k\), où \(k\) est un paramètre. Le point double est obtenu lorsque la valeur de \(k\) est nulle.

Toutes ces cubiques admettent l'axe des x comme axe de symétrie. Regardons donc comment elles coupent l'axe \(Ox\) d'équation \(y=0\). Les abscisses des intersections sont données en résolvant l'équation \(x^3+x^2=k\). Le premier membre de l'équation est une fonction de \(x\), un polynôme de degré impair. Quand \(x\) est très grand en valeur absolue (tend vers l'infini, positif ou négatif), seul le terme en \(x^3\) est important. Dans les corps des réels, nous aurons donc au moins une valeur de \(x\) qui annulera cette fonction. Soit a une valeur de \(x\) annulant le polynôme. Il sera alors divisible par \((x-a)\) et il restera une équation du second degré. En rassemblant ces résultats, cela signifie que sur les réels, une équation du 3e degré possède soit 3 solutions (quitte à ce que certaines soient confondues), soit une seule solution.

Comme il est malaisé de résoudre une équation générale du 3e degré , essayons de mieux caractériser les solutions de cette équation bien précise. Le cas simple est celui où le paramètre k est nul. Les solutions sont \(0\) (solution double) et \(-1\). Mais que se passe-t-il pour les autres valeurs de \(k\) ? L'équation qui donne les abscisses des points d'intersection de la cubique et de l'axe \(Ox\) est \(x^3+x^2=k\). Il suffit de l'écrire \(k=x^3+x^2\) pour avoir l'idée d'attaquer le problème d'une autre manière. Notons, pour éviter la confusion, \(F(x)=x^3+x^2\).

Le graphique de \(F(x)\) (en orange) résulte de la somme du graphique de \(x^3\) )en bleu) et de celui de \(x^2\) (en vert).

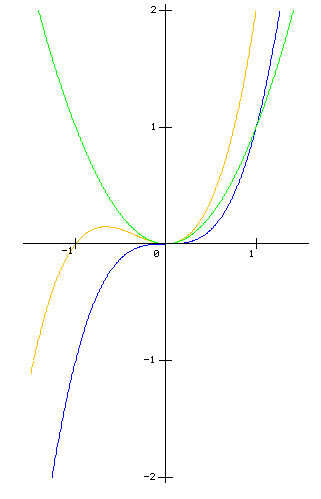\(F(x)=x^3+x^2\)

On observe 5 cas possibles : Si \(x\) est négatif, \(x^3\) est négatif mais \(x^2\) est positif. Tant que \(x\) est, en valeur absolue, supérieur à 1, \(x^2\) sera inférieur à \(|x^3|\) et la fonction \(F\) sera négative. Pour \(x=-1\), \(F=0\). Dès que \(x\) est, en valeur absolue, inférieur à \(1\), \(x^2\) sera supérieur à \(|x^3|\) et \(F\) devient positive. Si \(x=0\), à nouveau \(F=0\). Lorsque \(x\) devient positif les deux termes de la somme sont positifs et la fonction \(F\) est donc positive. En résumé: \(x\lt -1\) \(F\lt 0\) \(x=-1\) \(F=0\) \(-1\lt x\lt 0\) \(F\gt 0\) \(x=0\) \(F=0\) \(x\gt 1\) \(F\gt 0\)

On pourrait encore préciser cette étude de fonction à l'aide des dérivées; par exemple déterminer les coordonnées du maximum relatif de \(F(x)\) dans l'intervalle \([-1,0]\) (on préciserait que ce maximum est obtenu pour \(x=-2/3\) et vaut \(4/27\)).

Nous sommes à présent en mesure de répondre à la question posée plus haut : "Que peut-on dire des points d'intersection de la courbe \(x^3+x^2-y^2=k\) avec l'axe \(Ox\) ? "

Les abscisses de ces points étaient données par les solutions de l'équation : \(x^3+x^2-k=0\). Les intersections du graphique de \(F(x)-k\) avec l'axe Ox seront les solutions de l'équation du 3e degré. Le graphique de \(F(x)-k\) s'obtient à partir du graphique de \(F(x)\) par une translation parallèle à l'axe \(Oy\) d'amplitude \(-k\).

La réponse à la question posée plus haut se trouve à présent sous nos yeux.

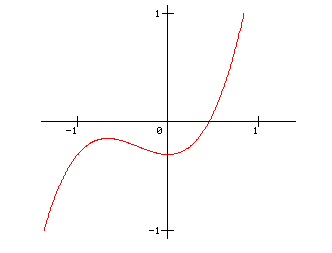
Détaillons le résultat (nous notons \(M\) le maximum de \(F(x)\) pour \(x \lt 0\)):

1. Pour \(k \lt M\), une seule solution positive.
2. Pour \(k = M\), nous avons deux solutions confondues en cette valeur.
3. Ensuite, lorsque \(M \lt k \lt 0\), ces deux valeurs se dissocient jusqu'à ce que la plus grande des deux soit égale à 0.
4. Pour \(k=0\), \(0\) est une solution double et l'autre est égale à \(-1\).
5. Lorsque \(k \gt 0\), il n'y a plus qu'une seule solution réelle négative.

Nous avons ainsi résolu et discuté cette équation paramétrique du 3e degré. Cela nous permet maintenant de préciser l'aspect de cette famille de cubiques. En effet, rappelons-nous que la famille des cubiques étudiées est donnée par \(y^2= x^3+x^2-k\) ou encore \(y^2=F(x)-k\). Il suffit donc de construire à partir du graphique de \(y^2\) celui de \(y\). Nous devons donc ajouter la condition \(x^3+x^2-k \ge 0\) ou encore \(F(x)\ge k\). Pour une valeur donnée de k seule la partie du graphique située au-dessus de l'axe Ox donnera lieu à des points de la cubique. La cubique sera obtenue en prenant la réunion des racines carrées positives et négatives du graphique de \(F(x)-k\) .

On voit que lorsque \(M\lt k\lt 0\), la partie positive est constituée de deux intervalles disjoints. Ces deux intervalles se rejoignent pour \(k=0\) et ensuite il n'y a qu'un seul intervalle où la fonction est positive. Comme \(y^2=x^3+x^2-k\), cela signifie que lorsque \(M\lt k\lt 0\), la courbe est donc également formée de deux parties disjointes. Pour \(k=0\), ces deux parties se rejoignent en un point double pour former la strophoïde et ensuite la courbe représentative est d'un seul tenant.

Voici une dernière animation qui montre ces cubiques d'équation \(x^3+x^2-y^2=k\) lorsque k varie de 0.3 à -0.5; elle s'attarde sur les deux valeurs remarquables \(4/27\) où la courbe possède un point double isolé pour \(x=-2/3\) et \(0\) où elle possède un point double à tangentes distinctes à l'origine.