Voici une petite curiosité qu'il serait dommage d'oublier, d'autant plus que lui sont associés les noms de deux mathématiciens, dont le célèbre Euler .

Soit un triangle de sommets \(p_1,p_2\) et \(p_3\). A ce triangle sont associés de nombreux points "remarquables". Accordons notre attention à 3 d'entre eux:

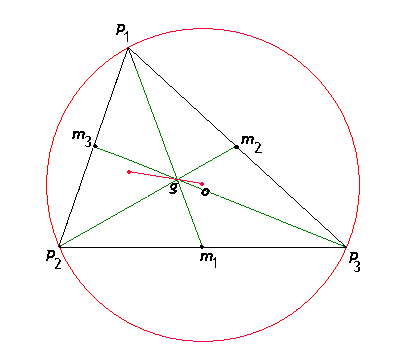
• \(o\), le centre du cercle circonscrit, intersection des 3 médiatrices,
• \(g\), le centre de gravité ( barycentre ), intersection des 3 médianes, et
• \(h\), l'orthocentre, intersection des 3 hauteurs.

S'il est très simple de montrer que les 3 médiatrices et que les 3 médianes sont concourantes, il est moins direct de montrer que les trois hauteurs d'un triangle concourent en un même point.

Pour cela on utilise une petite astuce. On remarque que les 3 médiatrices sont les 3 hauteurs du triangle ayant pour sommets \(m_1, m_2\) et \(m_3\), les 3 mileux des côtés du triangle initial. Il suffit alors de remarquer que l'on passe du grand triangle au petit par une homothétie de rapport \(-1/2\), dont le centre est situé au point \(g\), intersection des 3 médianes.

On voit ainsi que ce point \(g\) est aligné avec \(o\) et \(h\). La droite \(ogh\) est appelée droite d' Euler . De plus, comme le rapport d'homothétie vaut \(-1/2\), \(hg\) est le double de \(go\).

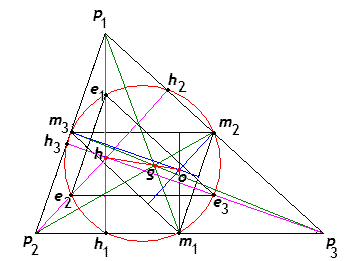
Sur cette figure on remarque également un cercle circonscrit au triangle \(m_1 m_2 m_3\).

Cliquez sur l'image pour démarrer l'animation.

On peut y voir des propriétés remarquables. Tout d'abord, ce cercle se déduit du cercle circonscrit au triangle \(p_1 p_2 p_3\) par une homothétie de rapport \(-1/2\) et de centre \(g\). Mais où est situé le centre \(f\) de ce cercle ? C'est évidemment l'image de \(o\) dans l'homothétie de centre \(g\) et de rapport \(-1/2\). On a déjà remarqué que \(hg=2go\), mais de plus \(fg=-1/2go\).

On a donc la configuration suivante:

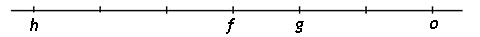
et le centre \(f\) est donc situé au milieu de \(ho\). Considérons à présent une homothétie de centre \(h\) et de rapport \(+1/2\).

Cliquez sur la figure pour démarrer l'animation.

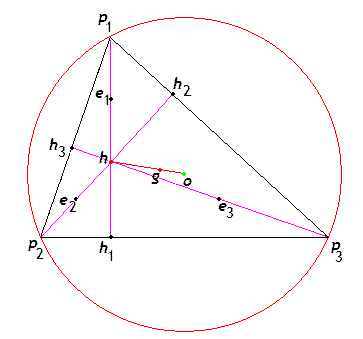
Cette homothétie transformera le cercle circonscrit à \(p_1 p_2 p_3\) en cercle de centre \(c\) et dont le rayon sera la moitié du cercle de départ. C'est donc le même cercle que le précédent ! Le triangle \(p_1 p_2 p_3\) a pour image le triangle \(e_1 e_2 e_3\) déterminé par les milieux de segments joignant chaque sommet à l'orthocentre; ces points sont appelés points eulériens. Il en résulte que les six points \(m_1, m_2, m_3\) et \(e_1, e_2, e_3\) sont situés sur un même cercle, ce qui est déjà fort remarquable.

Mais il y a plus ! Revenons à la figure initiale:

Le triangle \(e_1 e_2 e_3\) et le triangle \(m_1 m_2 m_3\) sont tous deux homothétiques au triangle \(p_1 p_2 p_3\). Les rapports d'homothétie valent respectivement \(+1/2\) et \(-1/2\). Ils sont donc homothétiques entre eux de rapport \(-1\), ce qui est équivalent à dire qu'ils se correspondent dans une symétrie centrale. De plus, le centre de symétrie est précisément le point \(f\). On voit donc que les points eulériens sont diamétralement opposés aux milieux des côtés du triangle et, par suite, les droites \(e_im_i\) qui les joignent sont des diamètres du petit cercle. Les triangles \(e_i, h_i, m_i\), pour \(i=1,2,3\) sont rectangles en \(h_i\) et il en résulte que les 3 points \(h_i\) sont également situés sur ce cercle. On a donc 9 points sur un même cercle !

Ce cercle des 9 points est également dénommé cercle de Feuerbach en l'honneur du mathématicien qui remarqua cette propriété.