Cette figure, étudiée par Viviani , a été utilisée en architecture pour la construction de coupoles. Elle est définie par l'intersection d'une sphère et d'un cylindre tangent dont le diamètre vaut le rayon de la sphère.

Soit une sphère \(S\) de rayon \(R\) et un cylindre \(C\) de rayon R/2 tangent à la sphère \(S\). La courbe \(S\cap C\) intersection de ces deux surfaces est appelée courbe de Viviani. 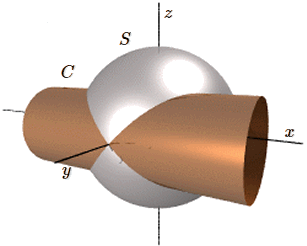En choisissant un système de coordonnées dont l'origine est au centre de \(S\) tel que l'axe de \(C\) soit parallèle à \(ox\) et le point de contact sur l'axe \(oy\), on obtient:

\(S \equiv x^2+y^2+z^2=R^2 \\ C \equiv y^2+z^2=Ry \)

La projection de la courbe sur le plan \(xoy\) est la courbe d'équation: \(x^2+Ry=R^2\) c'est-à-dire une parabole. Quant aux équations paramétriques de la courbe d'intersection de \(S\) et de \(C\), elles valent:

\[ \begin{cases} x = u \\ y = R~(1+\mathbf{cos~}\theta)/2 \\ z = R~\mathbf{sin~}\theta/2 \end{cases} \]

ce qui correspond aux équations de \(C\), avec la condition \(u^2=R^2(1-\mathbf{cos~}\theta)\) qui exprime que les points appartiennent à \(S\).

Projetons à présent cette courbe à partir du point \((0, -R, 0)\) sur le plan \(>xoz\). On obtient la courbe d'équation:

\[ (x^2+z^2)^2-R^2(x^2-z^2) = 0 \]

Cette équation est celle de la lemniscate de Bernoulli. Cette courbe remarquable représente l'ensemble des points d'un plan dont le produit des distances à 2 points fixes est constant et vaut le carré de leur demi-distance. En effet, soient dans le plan \(xoz\) les deux points d'abscisse \(\pm c\) sur l'axe \(ox\). Le carré du produit des distances d'un point de coordonnées \((x, z)\) vaut \(((x - c)^2 + z^2)((x + c)^2 + z^2)\), ce qui peut s'écrire \((x^2 + z^2 + c^2)^2 - 4c^2x^2\). Si le carré du produit des distances vaut \(c^4\), on obtient: \((x^2 + z^2)^2- 2c^2(x^2-z^2)=0\). Dans le cas présent \(c = R\sqrt{2}/2\)

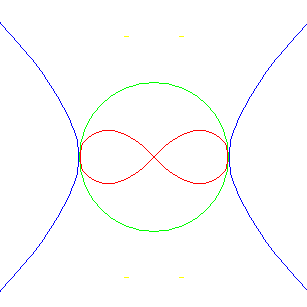
Projetons à présent la courbe de Viviani à partir de son point double \((0,R,0)\) sur le plan \(xoz\). On obtient cette fois \(x^2-z^2=R^2\). C'est l'équation d'une hyperbole équilatère. D'autre part, on sait que les projections à partir des deux points diamétralement opposés d'une sphère sur le plan diamétral perpendiculaire à la droite qui les joint, donnent des figures transformées par inversion .

On a ainsi prouvé que l'inverse d'une lemniscate de Bernoulli par rapport à son point double est une hyperbole.

Remarquons qu'un raisonnement plus synthétique peut conduire au fait que la projection à partir du point double est une hyperbole. En effet \(S\) et \(C\) sont deux quadriques. Dans le faisceau qu'elles déterminent, il existe 4 cônes (ou cylindres); l'un est \(C\), un autre est le cylindre projetant la parabole; les deux derniers cônes sont confondus puisque la courbe de Viviani possède un point double qui est d'ailleurs le sommet du cône.

La projection est donc une section conique, une hyperbole dans ce cas.