L'origami consiste en une manière de plier ( "ori" = plier = ) du papier ("gami" = papier = ) pour construire des figures plus élaborées. Une des règles du jeu est de s'interdire de découper ou de coller le papier, ce qui limite évidemment les marges de manœuvre. Cependant l'ingéniosité de certains a permis de réaliser des petites merveilles.

Partons d'une feuille quelconque. Il n'est guère difficile de construire un rectangle, un carré, un losange. En effet un pli dans une feuille de papier correspond d'une part à une droite, d'autre part à une symétrie axiale. Dès lors on peut construire les axes de symétrie d'une droite et par suite les perpendiculaires. Donc faire un angle droit n'est guère difficile. De plus construire une parallèle est également fort simple. On arrive donc très facilement à construire les quadrilatères ci-dessus.

De plus on peut aisément reporter des longueurs égales: un pliage amène une extrémité du segment sur la correspondante et un deuxième pliage achève d'amener l'autre extrémité en place. En fait, on peut pratiquement faire avec des pliages tout ce que l'on peut construire avec une latte et un compas.

Partons d'un carré. Est-il possible de construire un carré dont l'aire est la moitié de celle du carré de départ ? Très simple: il suffit de replier les 4 sommets sur le centre du carré. Peut-être est-ce plus difficile de construire un carré valant le tiers du carré initial ? Mais ce n'est pas impossible. Si on demande un carré valant le quart cela redevient simple. Bien sûr, on peut faire compliqué en se disant: "Puisqu'on sait construire la moitié, il suffit de prendre la moitié de la moitié." Mais évidemment il y a plus simple on replie le carré initial suivant ses médianes. 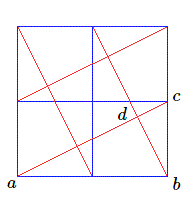Et si on demandait un carré égal au cinquième du carré initial ? Là encore on peut s'en tirer facilement. Il suffit de construire les médianes, et de replier suivant une droite joignant un sommet au milieu du côté opposé, comme le montre la figure. On voit immédiatement la carré central; la juxtaposition d'un trapèze avec un triangle donne un carré égal. Au total 5 carrés (attention un seul est obtenu sans découpage !) égaux. Un autre manière de le démontrer consiste à calculer le côté du carré central et le théorème de Pythagore est là pour nous donner un sérieux coup de main. Par exemple, si on prend pour unité un demi-côté du carré initial, le segment joignant un sommet au milieu du côté opposé vaut \(\sqrt{5}\). D'autre part dans le triangle rectangle \(abc\), la hauteur \(db\) le partage en 2 nouveaux triangles rectangles semblables. En particulier le triangle \(abd\) est semblable à \(acb\) et le rapport \(ab/ac=ad/ab\). On en déduit \(ad=ab^2/ac=4/\sqrt{5}\). Le côté du petit carré en vaut la moitié \((2/\sqrt{5}\)) et son aire est égale à \(4/5\), c'est-à-dire le cinquième de celle du grand carré. Cette seconde démonstration est plus compliquée que la première, mais elle met en lumière l'importance du théorème de Pythagore et montre que grâce à son usage répété, on peut aisément construire les racines carrées de tout naturel.

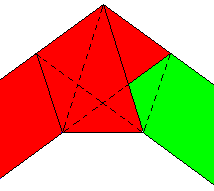Un autre exemple est de partir d'une bande de papier (assez étroite) et de former un nœud que l'on aplatit. On obtient ainsi quelque chose qui ressemble à un pentagone régulier. Reste à le démontrer...

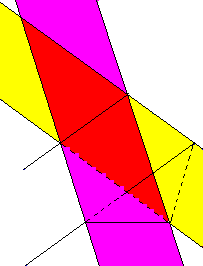Il suffit tout d'abord d'observer la symétrie de la figure et ensuite de s'intéresser à l'intersection de deux bandes de même largeur. On obtient comme intersection un losange, d'où de nombreuses égalités de segments et d'angles.

Ces deux exemples montrent comment réaliser simplement de petites constructions. De nombreuses autres peuvent être ainsi faites de manière fort élémentaire.

Sortant légèrement des règles de l'origami, autorisons-nous à recoller les extrémités de la bandelette de papier. Si nous recollons les extrémités soigneusement, en évitant que la bande ne soit tordue, nous obtenons évidemment un cylindre. Par contre, si nous recollons après lui avoir fait faire un demi-tour, le résultat est un ruban de Möbius , curieuse surface qui ne possède qu'une seule face et un seul bord. On peut ensuite poursuivre l'expérience en recollant après un tour, un tour et demi... et examiner les diverses surfaces obtenues.

Imaginons ensuite que l'on découpe longitudinalement en son milieu l'objet obtenu. Qu'obtient-on ? Pour le cylindre c'est assez évident: deux petits cylindres. Quant au ruban de Möbius, il vaut mieux réfléchir avant de répondre. Ensuite on peut vérifier à l'aide d'une paire de ciseaux (ce n'est bien entendu plus de l'origami !). Le résultat est surprenant. Compliquons légèrement les choses et coupons la bandelette longitudinalement à partir de son tiers. Quel sera le résultat ? Et ainsi de suite.

Bref voila de quoi s'occuper une après-midi pluvieuse !...