Nous vous présentons quelques surfaces construites à partir d'un rectangle (il s'agit en fait de propriétés topologiques, nous supposerons donc que le rectangle est fabriqué dans une matière déformable).

Etant donné un rectangle, on peut recoller deux côtés opposés de deux manières différentes: en identifiant les points se correspondant dans la symétrie axiales (manière la plus usuelle)

ou en identifiant les points se correspondant dans la symétrie centrale (en effectuant un ½ tour).

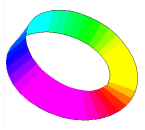Dans le premier cas on obtient un cylindre, dans le second une surface plus curieuse: le ruban de Möbius .

Que se passe-t-il si on essaye de fermer la surface en recollant les deux paires de côtés opposés du rectangle ? (Ce sera peut-être impossible à réaliser dans l'espace à 3 dimensions, mais on peut l'imaginer si on accepte que la surface peut s'interpénétrer)

Trois cas sont possibles:

1. On recolle chaque paire de la manière usuelle
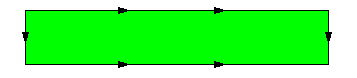
2. On recolle une paire de la manière usuelle et l'autre en effectuant un ½ tour
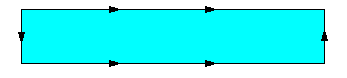
3. On effectue ½ tour pour chacune des paires de côtés opposés.

On obtient trois surfaces intéressantes. Elles sont représentées ci-dessous. Pour mieux les visualiser, un "clic" sur l'image vous amènera sur une vidéo !

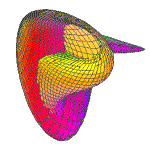
1. Tore	2. Bouteille de Klein	3. Surface de Boy

1. Le tore: C'est tout simplement la chambre à air d'un pneu.
2. La bouteille de Klein: Vous aurez de la peine à la remplir !
3. La surface de Boy: Une représentation tridimensionnelle du plan projectif.