Une méthode mathématique, souvent utilisée pour résoudre des problèmes pour lesquels il n'existe pas de méthode exacte directe, est la méthode d'itération.

Le principe de cette méthode est fort simple: on part d'une valeur (approchée, estimée) et, à partir d'une formule qui permet de l'améliorer, on construit une nouvelle valeur plus précise. On répète cette opération, autant de fois que nécessaire pour arriver à une précision suffisante. Un exemple est celui de la recherche de solutions d'une équation.

Nous avons déjà rencontré cette démarche lors de la recherche de la racine carrée (méthode de Platon, méthode de Héron) ainsi que celle de la recherche d'une racine n ^ème (méthode de Newton). Rappelons brièvement la méthode de Héron, dont la convergence est fort rapide.

Soit à calculer la racine carrée de \(n\) (évidemment > 0). On part d'une valeur approchée \(x_1\). Une manière de vérifier la vraisemblance de cette valeur est de calculer \(n/x_1\). Si le résultat est supérieur, nous avons sous-estimé cette racine, s'il est inférieur, nous l'avons surestimée. L'amélioration consiste à prendre alors une nouvelle valeur comprise dans l'intervalle déterminé par \(x_1\) et \(n/x_1\), par exemple la moyenne arithmétique. La nouvelle approximation \(x_2 = ( x_1 + n/x_1)/2 = (x_1^2 + n)/2x_1\).

Comment visualiser cette situation ?

Considérons tout d'abord la fonction \(y = (x^2 + n)/2x\) . En effectuant la division par \(2x\), on obtient \(y = x /2 + n/2x\). La fonction est donc la somme de \(y = x/2\) et de \(y = n/2x\). On peut utiliser cette information pour en construire le graphique . Pour simplifier la suite du dessin nous choisirons \(n=2\).

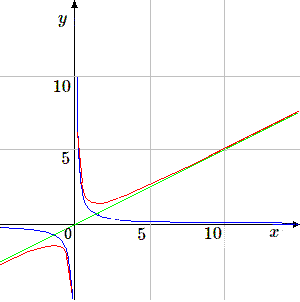
Dès que \(x\) est "grand" la fonction est proche de \(y = x/2\). La droite \(y = x/2\) représente la fonction asymptote. Par contre, au voisinage de \(x = 0\) il y aura une forte perturbation : la fonction sera infinie (positive) pour \(x>0\) ; ensuite elle sera décroissante et poursuivra son tracé en s'approchant de son asymptote \(y = x/2\).

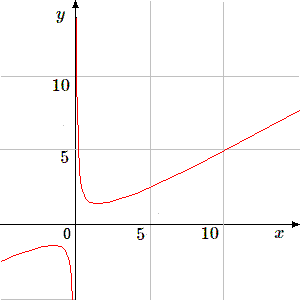
Le processus d'itération s'effectue de la manière suivante.

Partant de \(x_1\) on calcule la valeur \(y_1\) de cette fonction. Ensuite on prend \(x_2 = y_1\), c'est-à-dire qu'on utilise une deuxième fonction \(y = x\). On recommence l'opération avec la valeur \(x_2\) et ainsi de suite.

Représentons les choses graphiquement.

Evidemment, il n'y aucun problème pour représenter la fonction \(y = x\). Nous sommes maintenant à même de visualiser l'itération. Choisissons une valeur quelconque \(x_1 = 4\); à cette valeur correspond \(y_1 = 2,25\);

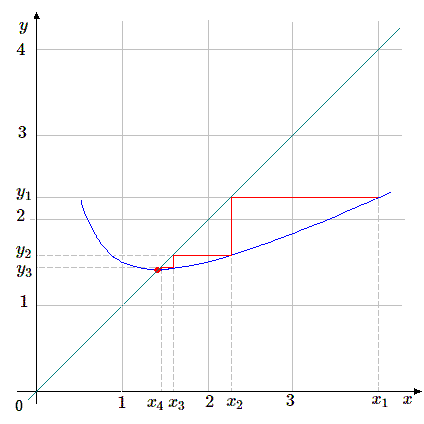
Essayons à présent \(x_2 = y_1 = 2.25\); on obtient \(x_3 = 1.5694444...\). En poursuivant on a: \(x_4 = 1.42189036..., x_5 = 1.41423428...\)

On obtient ainsi une suite de segments qui convergent vers le point de coordonnées \((a, a)\), solution du problème. Remarquons que ce point correspond au minimum de la fonction qui, on le vérifie facilement, est \(\sqrt{2}\).

Dans l'exemple choisi, on est certain d'aboutir à une valeur aussi précise que possible; cela se devine aisément à la vue du graphique. Cependant, ce n'est pas la panacée. Dans d'autres problèmes, la convergence n'est pas toujours assurée et il convient toujours de rester prudent.