Qu'y a-t-il de plus dissemblable que les points et les nombres ?

Les points (d'une droite, d'un plan, de l'espace à 3 dimensions) sont tous pareils - Les nombres rationnels, réels, complexes (nous songeons ici à un corps) sont tous différents.

Deux points distincts appartiennent à une unique droite - Deux nombres distincts (ou égaux !) peuvent être additionnés, multipliés.

Et on pourrait continuer à énumérer toutes les différences entre ces deux familles d'êtres mathématiques. Après tout, les points s'étudient en géométrie et les nombres en algèbre. N'est-ce pas suffisant pour montrer leurs différences ?

Mais il conviendrait toutefois d'être attentif au fait qu'on coordonne les points à l'aide de nombres et que ces coordonnées (des nombres) permettent de déterminer des points.

Alors qu'en est-il ?

Addition et translation - Multiplication et homothétie

Il est de fait qu'un lien existe entre les opérations sur les nombres et certaines transformations géométriques.

Prenons par exemple une droite (ensemble de points) munie d'un repère. A tout point correspond alors un nombre. Une translation sur cette droite qui applique le point de coordonnée 0 sur le point de coordonnée a, appliquera le point de coordonnée x sur le point de coordonnée x + a.

Voila un lien entre une translation et une addition.

Et si on effectue une multiplication (le point de coordonnée 0 ne bouge pas) le point de coordonnée 1 est envoyé sur le point de coordonnée k. Cette homothétie applique le point de coordonnée x sur le point de coordonnée k*x.

Un lien, cette fois, entre homothétie et multiplication.

Nous arrivons donc à la conclusion que même s'il y a bien des différences entre les points et les nombres, il existe quelques liens entre les opérations d'addition et de multiplication des nombres et les translations et homothéties.

La droite

Commençons par une droite. Comment pourrait-on définir une translation (ou une homothétie) ?

Une translation est définie par un point p et son transformé p' (ou encore un vecteur pp' ).

Mais pratiquement nous nous trouvons fort dépourvus lorsqu'on nous donne ce vecteur pp' et qu'on nous demande de construire un vecteur équipollent d'origine q . Au mieux nous pouvons prendre une latte et mesurer pp' et reporter (comment ?) cette mesure à partir du point q . Mais cela n'est pas bien sérieux ! Nous utilisons les nombres figurant sur notre latte pour construire la translation.

Le plan

Cette fois nous sommes plus à l'aise.

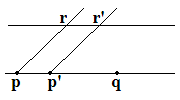
Si notre droite est plongée dans un plan, étant donné le vecteur pp' et un autre point q , nous pouvons ranger notre latte et il y a un moyen géométrique de construire q' .

Par les points p et p' construisons deux parallèles dans une direction distincte de celle de la droite et menons une parallèle à celle-ci. Nous obtenons un parallélogramme et le coté rr' opposé à pp' est un vecteur équipollent au vecteur pp' .

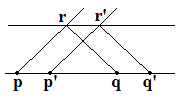
Par l'extrémité r , traçons la droite rq et par l'autre extrémité r' traçons la parallèle à cette droite. Elle coupera la droite en le point q' et nous aurons ainsi obtenu le vecteur qq' équipollent à pp' .

Malheureusement il y a bien trop d'arbitraire dans notre construction ! Nous avons fait choix d'une direction pour les deux parallèles initiales, ainsi que pour la parallèle à pp' . Sommes-nous assurés d'obtenir le même résultat en modifiant nos choix ? Hélas ! la réponse est négative.

Que se passerait-il si les choix étaient modifiés ?

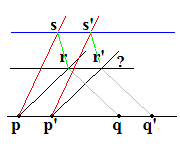
Modifions la direction de la droite issue de p ainsi que la parallèle à pp' . Nous obtenons le vecteur ss' . Mais, avant de poursuivre la construction, une question se pose: ce vecteur est-il équipollent à rr' ? En se basant sur les seules propriétés d'incidence des points et des droites, il est vain d'espérer pouvoir répondre affirmativement. En effet, on voit apparaître un cas (particulier) du théorème de Desargues. Les deux triangles prs et p'r's' ont des sommets homologues situés sur des parallèles ( pp' , rr' et ss' ); les côtés pr et p'r' sont parallèles; de même les côtés ps et p's' . Peut on en déduire que rs et r's' sont parallèles ?

Or dans le plan, il est bien connu que le "théorème" de Desargues est indémontrable et doit être ajouté comme axiome si on souhaite obtenir un plan "convenable".

Bref, tout s'effondre et nous sommes dans l'impossibilité de démontrer l'existence de translations (ce qui est équivalent à la construction raisonnable de vecteurs équipollents).

Donc, il est inutile de nous attaquer aux homothéties, la situation est perdue d'avance.

L'espace à 3 dimensions

Ici l'obstacle à la définition des translations disparaît. En effet le théorème de Desargues peut être démontré dans l'espace à 3 dimensions sur seule base des propriétés de linéarité (propriétés d'incidence et de parallélisme des points, droites et plans).

Qu'en est-il des homothéties (associées à la multiplication) ? 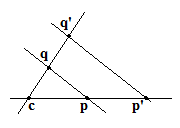Prenons un centre c d'homothétie et donnons-nous un point p et son transformé p' situé sur la droite cp ; en principe nous devons être capables de trouver les transformés de tout autre point par cette homothétie. Si un point q n'est pas situé sur la droite cpp' , construisons la droite pq ; sa transformée sera la parallèle passant par p' et q' sera sur la droite cq . (au cas où le point q serait sur la droite cp , on passerait par un point intermédiaire extérieur).

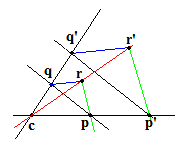
Dans l'espace, nous sommes à même de définir correctement cette homothétie. En effet si on construit l'image r' d'un autre point r , avec p'r' parallèle à pr , le théorème de Desargues (et rappelons qu'à 3 dimensions c'est bien un théorème, c'est-à-dire une propriété démontrable sur seule base des propriétés d'incidence et de parallélisme des points, droites et plans) nous garantit que la droite q'r' sera bien parallèle à qr .

Nous avons donc défini correctement l'ensemble des dilatations (translations et homothéties) de l'espace à 3 dimensions.

En particulier, nous pouvons fixer notre attention sur une droite et observer le groupe des dilatations conservant cette droite; il comprend toutes les translations amenant un point de la droite sur un autre point de celle-ci, ainsi que les homothéties centrées sur cette droite.

De plus, nous voyons que le groupe des translations (ou si l'on préfère le groupe additif des vecteurs) est commutatif. Pour deux translations de directions différentes, c'est évident, cela découle des propriétés du parallélogramme. Et si, par hasard, elles ont la même direction, il suffit d'intercaler une translation de direction différente suivie de son inverse. En effet:

$$ \begin{align} & T_1+T_2 = T_1+(T_3-T_3)+T_2 = (T_1+T_3)+(-T_3+T_2) \\ & = (-T_3+T_2)+(T_1+T_3) = (T_2-T_3)+(T_3+T_1) \\ & = T_2+(-T_3+T_3)+T_1 = T_2+T_1 \end{align} $$

Remarque importante: Nous ne sommes pas en mesure de prouver que l'ensemble des homothéties de même centre est commutatif.

Il est évident qu'une homothétie transforme une translation en une autre, de même direction mais d'amplitude différente. Donc le sous-groupe des translations est invariant dans le groupe des dilatations.

Quelques propriétés générales

Nous venons de rencontrer des groupes de permutations: translations, homothéties de même centre.

Sur une droite ces groupes ont une propriété commune:

• Il existe une et une seule translation qui amène un point sur un autre.
• Il existe une et une seule homothétie de centre donné qui amène un point sur un autre (les deux étant distincts du centre).

Que peut-on faire avec des groupes de permutations ayant cette belle propriété ?

Rappelons qu'un groupe G de permutations est un ensemble de permutations d'un ensemble E qui contient la composée de deux permutations quelconques de G et la réciproque de toute permutation de G .

Prenons donc un tel groupe qui, de plus, possède la propriété qu'il n'existe qu'une et une seule permutation du groupe appliquant un point sur un autre. (D'une manière "savante" on dit de ces groupes qu'ils sont simplement transitifs) Pour support intuitif, on peut songer aux exemples rencontrés plus haut (translations, homothéties de même centre sur une droite,...) et pour soutenir notre intuition nous appellerons points les éléments de E .

Dans l'ensemble E , choisissons un point quelconque \(n\).

A partir de là, nous définissons une loi sur les points de E , notée *. Dès lors, \(a*b\) est, par définition, l'image du point \(b\) par la permutation (unique) \(P_a\) de G qui applique \(n\) sur \(a\). Autrement dit \(a*b = P_a(b)\).

Quelles sont les propriétés de cette loi * ?

• Elle est évidemment toujours définie quels que soient les points \(a\) et \(b\) de E .
• Cette loi est associative.

en effet: \(a*(b*c)= P_a(b*c)= P_a\circ P_b(c)\) mais les permutations P appartiennent au groupe G ; donc \(P_a\circ P_b=P_x\) ; comment trouver x ? \(P_a\circ P_b(c) = P_x(c)\) d'où \(P_a(b*c) = x*c\) ou encore \(a*(b*c) = x*c\) cette relation est valable quel que soit \(c\); en particulier si \(c=n,~~ a*(b*n) = x*n\) et donc \(a*b = x\) Remplaçons \(x\) par sa valeur \(a*b\), on obtient: \(a*(b*c) = (a*b)*c\) ce qui prouve l'associativité de la loi *

• \(n\) est un élément neutre pour la loi \(a*n = P_(n)\) par définition. \(n*a = P_n(a)\); où \(P_n\) est la (seule) permutation qui fixe \(n\), donc la permutation neutre et \(n*a = a\)
• tout élément \(a\) possède un inverse \(a'\) tel que \(a*a' = a'*a = n\) ; il suffit de remarquer que si \(a*a' = P_a(a') = n\), on a: \(a' = P_a^{-1}(n)\)

Conclusion: pour tout groupe de permutations G strictement transitif sur E , après avoir fait choix d'un point quelconque n de E , la loi: a*b = P _a (b) définit sur les points de E une structure de groupe de neutre n.

Application aux points d'une droite de l'espace

Choisissons une droite de l'espace.

Nous avons vu que les translations formaient un groupe simplement transitif (et de plus commutatif). D'après ce que nous venons de voir, si nous choisissons un point 0 (le point désigné par \(n\) dans la généralisation) nous pouvons définir sur les points de la droite une loi que nous noterons +.

L'ensemble des points de la droite où l'on a choisi un point 0, muni de cette loi + aura une structure de groupe (commutatif) de neutre 0. Nous appellerons cette loi l'addition.

De même, choisissons sur cette droite un point distinct de 0 que nous appellerons 1. Les homothéties de centre 0 forment un groupe simplement transitif sur les points différents de 0. Nous pouvons ainsi définir une deuxième loi que nous noterons *. L'ensemble des points, à l'exception du point 0, sera ainsi muni d'une deuxième loi de groupe de neutre 1 que nous appellerons multiplication .

Pour 0, qui est fixe pour toutes les homothéties \(H_a\), on a \(H_a(0) = 0\) ce qui s'écrit \(a*0=0\). L'homothétie \(H_0\) n'est pas une permutation; tous les points d'appliquent sur \(0\) et on a donc, quel que soit \(a, H_0(a) = 0\) ou \(0*a = 0\).

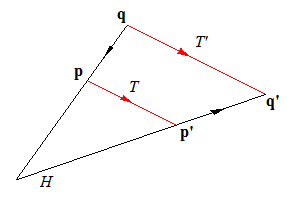
Reste à voir ce qu'apporte la propriété du sous-groupe des translations d'être invariant dans le groupe des dilatations, et en particulier invariant par le groupe des homothéties centrées en 0.

En fait, être invariant signifie qu'une translation T est transformée par une homothétie H en une translation T'

Pour déterminer la translation T' , il suffit de chercher p , l'image inverse de q par \(H^{-1}\), de prendre son image p' par la translation T et de lui appliquer l'homothétie H qui l'envoie sur q' ; cela se traduit par \(T' = H\circ T\circ H^{-1}\).

Choisissons une homothétie \(H_a\) et une translation \(T_b\), et nous obtenons: \(H_a\circ T_b\circ H_a^{-1} = T_x\) ou \(H_a\circ T_b = T_x\circ H_a\)

Appliquons cette permutation à un point c; il en résulte, en appliquant les définitions:

\[ H_a\circ T_b(c) = T_x\circ H_a(c) \text{ ou } H_a(c+b) = T_x(a*c)\]

c'est-à-dire \(a*(c+b) = a*c+ x\)

Comme cette relation est vraie quel que soit le point (le nombre ?) \(c\), et en particulier pour \(c = 0\) il vient: \(a*b = x\).

Réécrivons la propriété et nous obtenons:

\[a*(c+b) = a*c+ a*b\]

c'est-à-dire la distributivité à gauche de la multiplication par rapport à l'addition.

Remarque Si le groupe des homothéties de même centre est commutatif, alors nous avons comme conséquence immédiate la distributivité à droite .

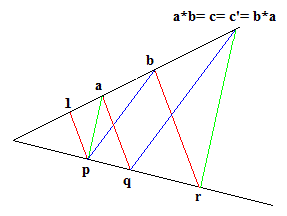
Géométriquement la commutativité de la multiplication est équivalente au théorème de Pappus.

En effet, l'homothétie appliquant 1 sur a (déterminée par le triangle 1pa) applique b sur c par l'intermédiaire du triangle brc. Mais l'homothétie appliquant 1 sur b (déterminée par le triangle 1pb) applique a sur le point c' par l'intermédiaire du triangle aqc' et le théorème de Pappus assure l'identité de c et de c'.

Conclusion

Alors, peut-être, nous faudra-t-il modifier notre introduction:

"Qu'y a-t-il de plus dissemblable que les points et les nombres ?"

et la remplacer par:

"Qu'y a-t-il de plus semblable que les points et les nombres ?"

A vous de juger !