Soit une application linéaire du plan donnée par les équations:

\[ \begin{cases} x'=ax+by \\ y'=c x+dy \end{cases}\]

Ces équations peuvent s'écrire sous forme matricielle :

\[ \left\lgroup\matrix{x'\\y'}\right\rgroup = \left\lgroup\matrix{a & b \\ c & d}\right\rgroup \left\lgroup\matrix{x\\y}\right\rgroup \]

Pour être assuré d'avoir à faire avec une permutation, on doit évidemment pouvoir calculer \(x\) et \(y\) en fonction de \(x'\) et de \(y'\); le déterminant \(D = ad-bc\) de la matrice doit donc être non nul.

Cette permutation agit sur les points et les droites du plan. L'origine est fixée et, par conséquent toutes les droites qui passent par l'origine le sont également. Demandons-nous si, par hasard, il n'existerait pas une droite conservée par l'application. Pour cela il suffit que l'image de l'un de ses points soit alignée avec le point et l'origine, c'est-à-dire que les coordonnées du point-image soient proportionnelles aux coordonnées du point de départ.

Soit un tel point de coordonnées \((x, y)\). Les coordonnées \((x', y')\) de son transformé doivent être proportionnelles.

\[ \begin{cases} x'=kx \\ y'=ky \end {cases}\]

Ses coordonnées vérifient donc un système homogène de deux équations:

\[ \begin{cases}ax + by = kx \\cx + dy = ky \end {cases}\]

ou encore

\[ \left\lgroup\matrix{a-k & b \\ c & d-k}\right\rgroup \left\lgroup\matrix{x\\y}\right\rgroup =0\]

On sait qu'un tel système n'admet en général que la solution \((0, 0)\) sauf si les deux equations sont proportionnelles, c'est-à-dire si le déterminant du système est nul.

Le déterminant vaut: \((a-k)(d-k)-bc\) et \(k\) est donc solution de l'équation \(k^2-(a+d)k+(ad-bc)=0\) La somme des racines vaut \(a + d\) (la somme des éléments de la diagonale, appelée trace) et le produit \(ad-bc\) (le déterminant). Les solutions sont appelées valeurs propres, et les directions ou vecteurs invariants, directions ou vecteurs propres.

Soient \(k_1\) et \(k_2\), les deux solutions de cette équation, et considérons l'une d'elle (que nous noterons tout simplement \(k\)). Comme les deux équations sont proportionnelles prenons l'une d'entre elles: \((a-k)x+by = 0\) (si elle se ramenait à \(0=0\), on prendrait l'autre, et si c'était également le cas pour l'autre, il s'agirait tout simplement d'une homothétie !). La droite qu'elle représente est fixe. Vérifions:

\[ \begin{aligned} (a - k)x' + by' & = (a - k)(ax + by) + b(cx + dy)\\ & = (a(a - k) + bc)x + ((a - k) + d)by\\ & = (a(a - k) + (a-k)(d-k))x + ((a-k) + d)by\\ & = (a - k)(a + d - k)x + (a - k + d)by\\ & = (a + d - k)((a - k)x + by) \end{aligned} \]

On voit ainsi que le premier membre de l'équation d'une droite invariante correspondant à l'une des valeurs propres \(k\) est multiplié par \(a+d-k\), c'est-à-dire par l'autre valeur propre. Pour chacune des deux valeurs \(k_1, k_2\) de \(k\) on obtient une direction invariante. En posant:

\[ \begin{cases} X = (a-k_1)x + by \\ Y = (a-k_2)x + by \end {cases}\]

dans ce nouveau système de coordonnées l'application linéaire prend la forme simple:

\[ \begin{cases} X' = (a+d-k_1)X \\Y' = (a+d-k_2)Y\end {cases}\] ou \[ \begin{cases} X' = k_2X \\Y' = k_1Y\end {cases}\]

La transformation est devenue très facile à se représenter: \(X' Y' = k_1 k_2 X Y\) le coefficient vaut précisément le déterminant \(ad-bc\) de la transformation. Si le déterminant est négatif nous remplacerons \(k_2\) par \(-k_2\) et moyennant une symétrie par rapport à l'axe X, nous aurons des équations de la même nature.

\[ \begin{cases} X' = \alpha X\\ Y' = \beta Y \end {cases}\]

avec un produit \(\alpha \beta\) positif que nous posons égal à \(h^2\). La transformation est la composée d'une homothétie de rapport \(h\) et d'une transformation d'équations:

\[ \begin{cases} X' = \lambda X\\ Y' = \lambda ^{- 1} Y \end {cases}\]

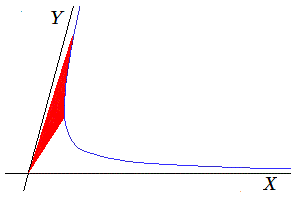
Les courbes d'équations \(X Y\) = constante, c'est-à-dire les hyperboles ayant les axes coordonnés comme asymptotes sont invariantes. Cette application linéaire est appelée "rotation hyperbolique".

L'application linéaire générale est donc la composée d'une rotation hyperbolique, d'une homothétie et, éventuellement d'une symétrie par rapport à un axe coordonné.

Tout cela est bien beau, mais à y regarder de plus près, pas très correct !

Nous avons travaillé avec une équation du second degré et nous avons supposé qu'elle possédait deux solutions réelles.

Ce n'est pas très grave, mais il faut vérifier ce qui se passe lorsque l'équation possède deux solutions égales (cas très particulier) ou deux solutions complexes conjuguées.

Regardons d'abord rapidement le cas exceptionnel où les deux solutions sont confondues. 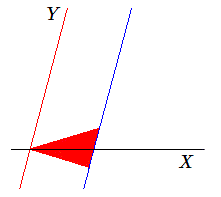Il n'y a alors qu'une direction invariante; prenons-la comme axe \(X\), et choisissons une autre direction comme axe \(Y\). Les équations deviennent:

\[ \begin{cases} X'=k X\\ Y'= mX+nY \end {cases}\]

mais comme il n'y a qu'une direction invariante \(n = k\), et que les équations sont le produit d'une homothétie de rapport k par un cisaillement parallèle à l'axe Y d'équations:

\[ \begin{cases} X' = X \\ Y' = pX + Y \end {cases}\]

Le cas où les deux solutions sont complexes conjuguées est plus amusant. Notons les deux solutions \(k\) et \(\bar k\) et remarquons que leur produit (le déterminant) est donc positif. Tous les calculs précédents restent valables et se simplifient. On a:

\[ \begin{cases} X = (a-k)X + bY \\Y = (a-\bar k)X + bY \end {cases}\] et \[ \begin{cases} X' = \bar k X \\Y' = k Y \end {cases}\]

Nous avons \(Y=\bar X\); (n'oublions pas que nous travaillons avec des axes coordonnés complexes !) Pas de panique; posons tout simplement:

\(X = U + i V\)  et   \(k=r (\mathbf{cos~} \varphi + i \mathbf{sin~} \varphi)\)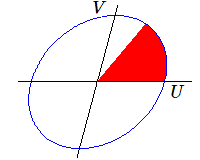

En séparant partie réelle et partie imaginaire, il vient:

\[ \begin{cases} U' = r.( U\mathbf{cos~} \varphi + V\mathbf{sin~} \varphi)\\ V' = r.(-U\mathbf{sin~} \varphi + V\mathbf{cos~} \varphi)\end{cases}\]

Comme dans le cas des deux racines réelles distinctes l'application est la composée d'une homothétie de rapport \(r\) et d'une rotation, non plus hyperbolique, mais elliptique. Nous retrouvons (si le repère est orthonormé) les équations d'une similitude.

Terminons par un mot au sujet des directions.

Si la droite n'est pas une direction propre:

• dans le cas de deux directions propres, ses transformées se rapprocheront de plus en plus de l'une des deux directions propres, de celle correspondant à la plus grande des 2 valeurs propres (en valeur absolue).
• si les deux valeurs propres sont égales, ses transformées se rapprocheront de l'unique direction propre.
• enfin, dans le cas où il n'y a pas de valeur propre réelle, la direction de la droite "tourne". Elle peut éventuellement revenir à sa position initiale dans le cas où l'argument du complexe k est un multiple rationnel de π.