Des élections vont avoir lieu la semaine prochaine. Les instituts de sondages s'en donnent à coeur joie, et... les résultats diffèrent. Comment expliquer cela ? Tout simplement parce qu'il est impossible d'interroger tous les électeurs (c'est justement pour cela qu'il y a des élections). On choisit un échantillon représentatif d'électeurs et d'après leurs avis on en déduit la tendance générale de la population.
La situation est pareille dans le cas de contrôle de qualité. Un producteur fournit des milliers de pièces en garantissant au maximum 2% de pièces défectueuses. Comme il est impossible de contrôler toute la fourniture on choisit un échantillon et en fonction des résultats on accepte ou on refuse le lot.
Voyons cela de plus près dans le cas d'un sondage préélectoral. Pour simplifier les choses nous supposerons que la population est très grande et que l'échantillon est formé de \(10\) personnes. Pour des raisons de commodité nous supposerons ces \(10\) personnes tirées indépendamment au hasard: il est donc possible de retrouver plusieurs fois la même personne. C'est évidemment hautement improbable si la population est importante.
Supposons que 90% de la population vote pour moi. Dans ce cas la probabilité \(p\) de tomber sur un "bon" électeur est de \(0,9\) et la probabilité \(q\) de tomber sur un "mauvais" est de 0,1.
Dans notre cas prenons un échantillon de (très petite) taille: \(n=10\) et réferons-nous à la distribution binomiale . On obtient la probabilité d'avoir \(k\) "bons" électeurs par la formule \(P_n(k)={n\choose k}p^{k}q^{n-k}\) avec \(p=0,9\) et \(q=0,1\) Il est facile de calculer la probabilité d'avoir \(10\) "bons", c'est-à-dire de relever une fréquence égale à \(1\); elle vaut \(1.0,9^{10}.0,1^0=0,349\). (en arrondissant à la troisième décimale) Un rien plus difficile : la probabilité d'avoir \(9\) "bons", c'est-à-dire d'avoir une fréquence \(0,9\), vaut \(10.0,1^9.0,9^1=0,387\). Avec un rien de patience (et une petite calculatrice !) on obtient le tableau suivant:
| Fréquence \(f\) relevée dans l'échantillon | \(0\) | \(0,1\) | \(0,2\) | \(0,3\) | \(0,4\) | \(0,5\) | \(0,6\) | \(0,7\) | \(0,8\) | \(0,9\) | \(1\) |
| \(p=0,9\) | \(0\) | \(0\) | \(0\) | \(0\) | \(0\) | \(.001\) | \(.011\) | \(.057\) | \(.194\) | \(.387\) | \(.349\) |
Dans ce tableau nous lisons que, \(p\) valant \(0,9\), la probabilité d'observer une fréquence \(f=0,8\) (c'est-à-dire d'avoir \(8\) "bons" électeurs sur les \(10\)) vaut \(0,194\). Nous pouvons également affirmer qu'il y a moins de \(10\)% de risque d'erreur d'avoir \(8, 9\) ou \(10\) "bons" électeurs dans l'échantillon choisi. En effet, la probabilité de relever une fréquence comprise entre \(0,8\) et \(1\) vaut \(0,194+0,387+0,349=0,930\gt 0,9\). Poursuivons les calculs pour d'autres valeurs de \(p\); nous nous limiterons ici aux valeurs décroissant de dixième en dixième.
On obtient le tableau suivant; la valeur \(p\) est disposée verticalement et les fréquences \(f\) observées sont reprises dans les lignes :
| \(p/f\) | 0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | \(0\) | \(0\) | \(0\) | \(0\) | \(0\) | \(0\) | \(0\) | \(0\) | \(0\) | \(0\) | \(1\) |
| 0,9 | \(0\) | \(0\) | \(0\) | \(0\) | \(0\) | \(.001\) | \(.011\) | \(.057\) | \(.194\) | \(.387\) | \(.349\) |
| 0,8 | \(0\) | \(0\) | \(0\) | \(.001\) | \(.006\) | \(.026\) | \(.088\) | \(.201\) | \(.302\) | \(.268\) | \(.107\) |
| 0.7 | \(0\) | \(0\) | \(.001\) | \(.009\) | \(.037\) | \(.103\) | \(.2\) | \(.267\) | \(.233\) | \(.121\) | \(.028\) |
| 0.6 | \(0\) | \(.002\) | \(.011\) | \(.042\) | \(.111\) | \(.201\) | \(.251\) | \(.215\) | \(.121\) | \(.04\) | \(.006\) |
| 0.5 | \(.001\) | \(.01\) | \(.044\) | \(.117\) | \(.205\) | \(.246\) | \(.205\) | \(.117\) | \(.044\) | \(.01\) | \(.001\) |
| 0.4 | \(.006\) | \(.04\) | \(.121\) | \(.215\) | \(.251\) | \(.201\) | \(.111\) | \(.042\) | \(.011\) | \(.002\) | \(0\) |
| 0.3 | \(.028\) | \(.121\) | \(.233\) | \(.267\) | \(.2\) | \(.103\) | \(.037\) | \(.009\) | \(.001\) | \(0\) | \(0\) |
| 0.2 | \(.107\) | \(.268\) | \(.302\) | \(.201\) | \(.088\) | \(.026\) | \(.006\) | \(.001\) | \(0\) | \(0\) | \(0\) |
| 0.1 | \(.349\) | \(.387\) | \(.194\) | \(.057\) | \(.011\) | \(.001\) | \(0\) | \(0\) | \(0\) | \(0\) | \(0\) |
| 0 | \(1\) | \(0\) | \(0\) | \(0\) | \(0\) | \(0\) | \(0\) | \(0\) | \(0\) | \(0\) | \(0\) |
Que pouvons-nous conclure grâce à ce tableau ? Pour une probabilité \(p=0,6\), il y a moins de \(10\)% de risque d'erreur d'affirmer qu'il y aura plus de \(3\) "bons" électeurs, et moins de \(10\)% de risque d'erreur qu'il y en ait moins de \(9\) dans l'échantillon choisi. Si on tolère un risque d'erreur de \(10\)% en plus ou en moins, on acceptera le fait que pour \(p=0,6\), il y aura entre \(4\) et \(8\) "bons" électeurs. S'il n'en est pas ainsi on rejettera l'hypothèse faite sur la valeur supposée de \(p\).
Résumons ces conclusions dans un tableau où nous ne garderons que les valeurs acceptables (avec un risque d'erreur de 10% en plus ou en moins).
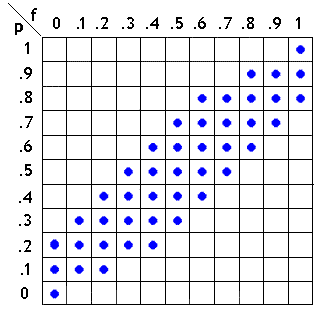
En lisant ce tableau "verticalement", on peut donc dire, par exemple, que si sur les \(10\) personnes interrogées, \(9\) affirment qu'elles voteront pour moi, la probabilité \(p\) est comprise entre \(0,7\( et \(0,9\( (à \(0,1\) près et un risque d'erreur de \(10\)%).
Il va de soi que cette méthode risque de devenir rapidement impraticable si l'échantillon est plus important. Heureusement, dans ce cas, on sait que l'on peut approcher la loi binomiale par une loi normale .
On dispose d'abaques reprenant les données avec le risque d'erreur toléré.
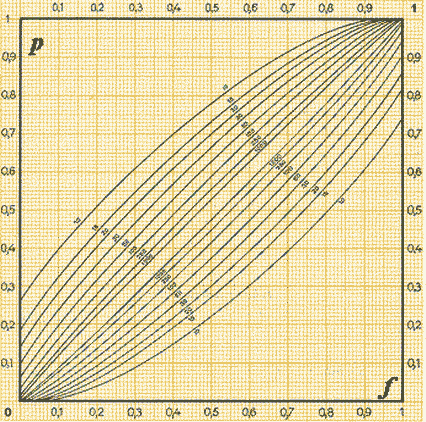
Ci-contre vous voyez une table correspondant à un risque d'erreur de \(10\)% (\(5\)% en trop, \(5\)% en moins). Sur les courbes sont indiquées les tailles des échantillons testés. A titre d'exemple, supposons un échantillon de \(50\) unités, et la fréquence \(f=0,7\) relevée. On en déduit, avec un risque d'erreur de \(10\)%, que \(p\) est compris entre 0.53 et 0.81.
On constate que la précision augmente évidemment avec la taille de l'échantillon; les courbes se resserrent lorsque \(n\) augmente. Par contre si on abaissait le risque d'erreur en le ramenant par exemple à \(5\)%, il est évident qu'il faudrait tester un échantillon de plus grande taille. Dans ce cas, on obtiendrait un système de courbes plus espacées.