Généralisons quelque peu la célèbre suite de Fibonacci , et supposons que chaque terme est, non pas la somme des deux précédents mais plus généralement, une combinaison linéaire des deux précédents.

\[ x_n=ax_{n-1} + bx_{n-2} \]

Quelle est la limite du quotient de 2 termes consécutifs de cette suite? Si cette limite existe, soit \(\varphi\) sa valeur; pour \(n\) suffisamment grand on a approximativement \(x_n \approx>\varphi x_{n-1}\) et \(x_{n-1} \approx \varphi x_{n-2}\) donc la relation de récurrence devient \(\varphi^2 x_{n-2} \approx \varphi ax_{n-2} + bx_{n-2}\) en simplifiant par \(x_{n-2}\) on a: \(\varphi^2 \approx \varphi a + b\) et \(\varphi \) doit être solution de l'équation:

\[ \varphi ^2 -a\varphi -b=0 \]

Il est clair que si cette équation n'a pas de solution réelle, la limite n'existe pas. On peut néanmoins s'interroger sur l'évolution du rapport \(x_n/x_{n-1}\) en fonction de \(n\).

En choisissant des exemples numériques on constate des comportements assez curieux suivant les valeurs choisies pour \(a\) et \(b\) (Remarquons que seul le rapport \(a^2/b\) importe!). Parfois même cette suite de rapports est périodique et, avec un peu de chance, on tombe facilement sur des valeurs donnant une périodicité d'ordre 3, 4, 6. Plusieurs questions se posent: peut-on obtenir n'importe quelle période? Comment choisir \(a\) et \(b\) ? Quelle est la nature de la relation entre \(a\) et \(b\) ? Essayons d'éclaircir ce problème.

Par exemple si \(a=1\) et \(b=-0.32\)

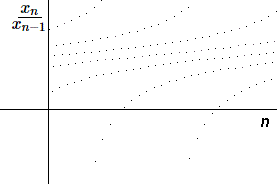
Quelques essais nous auront rapidement convaincus que les valeurs de départ \(x_0\) et \(x_1\) n'ont guère d'influence sur l'évolution à long terme du rapport \(x_n/x_{n-1}\). Exprimons les \(x_n\) en fonction de \(x_0\) et \(x_1\).

\[ \begin{align} x_2 & =ax_1 + bx_0 \\ x_3 & =ax_2 + bx_1 = a(ax_1 + bx_0) + bx_1 \\ & =(a^2 + b)x_1 + abx_0 \\ x_4 & =ax_3 + bx_2 = a[(a^2 + b)x_1 + abx_0] + b[ax_1 + bx_0] \\ & =(a^3 + 2ab)x_1 + (a^2b + b^2)x_0 \end{align} \]

etc.

On voit ainsi que \(x_n=P_n(a,b)x_1 +Q_n(a,b)x_0\), où \(P_n\) et \(Q_n\) sont 2 polynômes (de degré \(n-1\)) en \(a\) et \(b\). Que peut-on dire de ces polynômes ? Évidemment, ils satisfont à une condition qui découle de la définition même de la suite.

\[ x_n=a[P_{n-1}x_1+Q_{n-1}x_0]+b[P_{n-2}x_1+Q_{n-2}x_0] \\ =(aP_{n-1}+bP_{n-2})x_1+(aQ_{n-1}+bQ_{n-2})x_0 \]

c'est-à-dire:

\[ P_n=aP_{n-1}+bP_{n-2} \]

et de même pour les polynômes \(Q_n\). Ces derniers ne sont guère intéressants car si nous posons \(P_0=0\) et \(P_1=1\), nous voyons que \(Q_n=bP_{n-1}\). Nous pouvons donc oublier les polynômes \(Q_n\) et ne nous intéresser qu'aux \(P_n\).

On a donc:

\[ x_n=P_n x_1+bP_{n-1}x_0 \]

Voici l'expression des premiers polynômes \(P_n\) :

\[ \begin{align} P_0 & = 0\\ P_1 & = 1\\ P_2 & = a\\ P_3 & = a^2 + b\\ P_4 & = a^3 + 2ab\\ P_5 & = a^4 + 3a^2b + b^2\\ & ... etc. \end{align} \]

On voit apparaître une analogie avec le triangle de Pascal et on vérifie sans peine que les polynômes \(P_n\) s'obtiennent à partir du développement de \((a + b)^n\) en lisant le tableau "en oblique".

\[ 1 \\ a + b \\ a^2 + 2ab + b^2 \\ a^3 + 3a^2b + 3ab^2 + b^3 \\ a^4 + 4a^3b + 6a^2b^2 + 4ab^3 + b^4 \\ a^5 + 5a^4 b + 10a^3 b^2 + 10a^2b^3 + 5ab^4 + b^5 \\ .............................................. \]

On a:

\[ P_n(a,b) = {{n-1}\choose 0}  a^{n-1} + {{n-2}\choose 1}  a^{n-3}b + {{n-3}\choose 2}  a^{n-5}b^2 + ... \]

(il suffit de vérifier que \(P_1=1\) et \(P_2=a\) et que la relation de récurrence est satisfaite).

Revenons à la périodicité de la suite des rapports x _n / x n -1.

On calcule le rapport :

\[ \frac {x_n}{x_{n-1}} = \frac {P_n x_1 + b P_{n-1} x_0} {P_{n-1}x_1 + b P_{n-2}x_0} = \frac {P_n \frac{x_1}{x_0} + b P_{n-1}} {P_{n-1} \frac{x_1}{x_0} + b P_{n-2}} \]

Il y aura périodicité (de période \(n-1\)) si \(x_n/x_{n-1}=x_1/x_0=\lambda \)

c'est à dire:

\[ \lambda = \frac {P_n \lambda + b P_{n-1} } {P_{n-1}+ b P_{n-2} }\]

où \(\lambda P_n + bP_n-1 - \lambda^2 P_n-1 - b\lambda P_{n-2} = 0 ; ~~\text{mais}~~P_n = aP_{n-1} + bP_{n-2},\) d'où \(a\lambda P_{n-1} + b\lambda P_{n-2} + b P_{n-1} - \lambda^2 P_{n-1}- b\lambda P_{n-2} = 0 \), c'est-à-dire \((a\lambda+b-\lambda^2)P_{n-1} = 0\)

Nous sommes précisément dans le cas où cette équation n'a pas de solution réelle (à comparer avec l'équation en \(\varphi\) plus haut). Le polynome en \(\lambda \) ne peut être nul et donc \(P_n-1=0\). Le résultat est donc que la suite des rapports est périodique d'ordre \(n\) si \(P_n=0\). Inversement si \(P_n=0\) la suite des rapports est périodique, de période \(n\), et par conséquent \(P_{2n}= P_{3n} =....= 0\). Comme ces polynômes n'ont pas de racine multiple, l'ensemble \(P_n(a,b)\) possède donc la propriété remarquable que si \(m|n, P_m(a,b) | P_n(a,b)\).

Une étude plus approfondie de ceux-ci montrerait qu'ils possèdent tous (au moins) une racine réelle négative dont la valeur absolue est fonction décroissante de n ; les premières valeurs sont (pour a = 1)

\[ \begin{align} n~~~~~~ & b \\ 3~~~~~~ & -1 \\ 4~~~~~~ & -0.5 \\ 5~~~~~~ & -0.381966... \\ 6~~~~~~ & -0.333333... \\ 7~~~~~~ & -0.307978... \\ 8~~~~~~ & -0.292893... \\ 9~~~~~~ & -0.283118... \\ 10~~~~~ & -0.276393... \\ ...~~~~ & .... \end{align} \]

Lorsque la période \(n\) tend vers l'infini, la plus petite racine négative, en valeur absolue, tend vers -0,25 (voir suites récurrentes ).