Pendant de nombreux siècles, la géométrie euclidienne a été utilisée sans que l'on mette en doute sa validité; c'est à l'époque où les philosophes se posaient la question de l'unicité de l'espace que les recherches "parallèles" de Gauss , Bolyai et Lobatchevski ont conduit à la découverte de la géométrie hyperbolique; peu après les travaux de Riemann allaient mener à la géométrie elliptique. Depuis lors, Klein a donné une interprétation qui unifiait les 3 types de géométries métriques, euclidienne, elliptique et hyperbolique.

Rappelons le modèle de Klein relatif à la géométrie hyperbolique, c'est-à-dire la géométrie d'un plan possédant "presque toutes" les propriétés du plan euclidien, mis à part le fait que par un point extérieur à une droite on peut mener plusieurs parallèles.

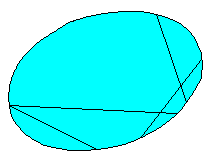
Les points du plan sont les points intérieurs à une conique d'un plan projectif. Les droites sont les segments de droite intérieurs à la conique.

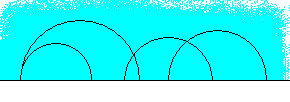
Poincaré , dans un tout autre contexte, a donné un modèle de la géométrie hyperbolique dans le plan de la variable complexe. Les points du plan sont les nombres complexes à partie imaginaire strictement positive, c'est-à-dire le demi-plan complexe supérieur ouvert. Les droites sont les cercles centrés sur l'axe réel; ces cercles sont par conséquent orthogonaux à la frontière.

On obtient une variante du modèle de Poincaré en utilisant une transformation homographique appliquant \(z\) sur \((az+b)/(cz+d)\), avec \(a,b,c,d\) complexes: l'axe réel se transforme en un cercle; de plus comme cette transformation est conforme, les "droites" se transforment en cercles orthogonaux, d'où une variante: les points du plan hyperbolique sont les points intérieurs à un cercle et les droites les cercles qui lui sont perpendiculaires.

Le groupe des projectivités conservant une conique est isomorphe au groupe des transformations homographiques, d'où une première démonstration de l'isomorphisme des deux modèles. Chacun de ces deux modèles présente des avantages et des inconvénients:

• le modèle de Poincaré est conforme; les angles sont respectés; par contre les droites se présentent sous l'aspect de cercles;
• le modèle de Klein est linéaire; les droites sont respectées, mais les angles sont déformés.

On peut montrer de manière élémentaire l'équivalence de ces deux modèles par construction d'un troisième modèle. Il est obtenu à partir d'une demi-sphère; les points du plan hyperbolique sont les points de la demi-sphère ouverte, et les droites sont les sections circulaires situées dans des plans perpendiculaires au plan limitant la demi-sphère.

À partir de ce modèle on retrouve les deux modèles décrits plus haut. En effectuant une projection parallèle orthogonalement au plan du cercle limite, on retrouve le modèle de Klein. Par contre si l'on projette stéréographiquement à partir d'un point de l'autre demi-sphère, on retrouve le modèle de Poincaré.

De même que le plan elliptique peut se représenter par une sphère, ou plus précisément par une sphère dont on identifie les points antipodes, on peut montrer un modèle métrique du plan hyperbolique (ou d'un morceau de plan hyperbolique) en construisant une surface à courbure constante négative, par exemple une pseudo-sphère (surface engendrée par la rotation d'une tractrice autour de son asymptote).