Construisons une suite de rectangles définie de la manière suivante. On part d'un rectangle quelconque. Sur son grand côté on construit un carré; ensuite en tournant toujours dans le même sens, on accole un carré sur le grand côté du rectangle obtenu à l'étape précédente; on poursuit indéfiniment l'opération. Que peut-on dire des figures obtenues ?

Si \(a_0\) et \(a_1\) sont les côtés du rectangle initial, les côtés du deuxième rectangle seront \(a_1\) et \(a_2=a_1+a_0\); de proche en proche on obtient \(a_n+1=a_n + a_n-1\). En particulier si \(a_0 = a_1 = 1\) on reconnaît la célèbre suite de Fibonacci : 1, 1, 2, 3, 5, 8, 13, 21...

Quel que soit le rectangle de départ, à une étape suffisamment grande de la construction on ne pourra plus "distinguer" celui-ci; le rectangle obtenu possédera une propriété particulière: si on lui enlève un carré construit sur son petit côté, il reste un rectangle semblable au rectangle précédent.

Calculons les proportions de ce rectangle, dit "rectangle d'or". Soit \(x\) le rapport du grand côté au petit côté. En choisissant ce dernier comme unité, et en retranchant un carré de côté \(1\), on obtient un rectangle de côtés \(1, x-1\) semblable au rectangle initial de côtés \(x, 1\). On a donc:

\[ x-1=\frac 1 x ~~~~ou~~~~x^2-x-1=0 \]

dont la solution positive est \(\tau=\Large\frac{\sqrt5 + 1}{2}\), appelé le nombre d'or.

On voit que de \(x-1=1/x\) on déduit \(x=1+1/x\); en remplaçant \(x\) par sa valeur on obtient:

\[ x=\frac{1}{1+\frac{1}{x}} \]

et en répétant on arrive à l'expression :

\[ x=\frac{1}{1+\frac{1}{1+\frac{1}{1+...}}} \]

Des approximations de \(\tau \) s'obtiennent comme "réduites" en arrêtant la fraction à un étage donné: on a successivement \(1, 2, 3/2, 5/3, 8/5,...\) c'est-à-dire les rapports de 2 termes consécutifs de la suite de Fibonacci. On voit ainsi que le rapport de 2 termes consécutifs de la suite tend vers le nombre d'or.

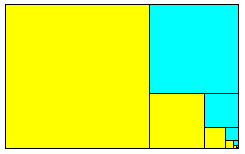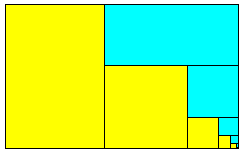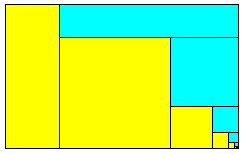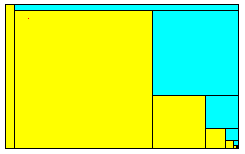Si d'un rectangle d'or, disposé sur son grand côté, on retranche sur la gauche un carré on obtient un rectangle semblable, mais disposé sur son petit côté. En retranchant un carré au-dessus de ce rectangle, on obtient un rectangle non seulement semblable, mais homothétique au premier. On obtient une suite infinie de tels carrés, ce qui se voit en zoomant sur le coin inférieur droit du rectangle initial.

De manière analogue construisons une suite de rectangles obtenus d'une manière semblable: la seule modification est qu'au lieu d'ajouter un carré, nous ajouterons à chaque étape, deux carrés égaux.

On aura alors la relation \(a_{n+1}=2a_n+a_{n-1}\). En particulier si \(a_0 = a_1=1\) on obtient la suite \(1, 1, 3, 7, 17, 41,...\) On peut également s'intéresser à la limite du rapport de 2 termes consécutifs de cette suite. Un calcul analogue à celui fait précédemment nous conduit à l'équation :

\[ x^2-2x-1=0 \]

qui admet pour solution positive \(x=\sqrt{2}+1\).

On obtient pour expression :

\[ \sqrt{2}+1=2+\frac{1}{2+\frac{1}{2+\frac{1}{2+...}}}~~~\text{ou}~~~~\sqrt{2}=1+\frac{1}{2+\frac{1}{2+\frac{1}{2+...}}} \]

d'où, pour \(\sqrt 2\), les approximations successives \(1, 3/2, 7/5, 17/12, 41/29,... \)

Par analogie avec le PGCD on voit que dans les deux cas ci-dessus ces rectangles ont des côtés incommensurables; en particulier \(\sqrt 2\) est un nombre irrationnel. Cette démonstration de l'irrationalité de \(\sqrt 2\) est très proche de celle des Grecs. En fait ils construisaient la figure suivante:

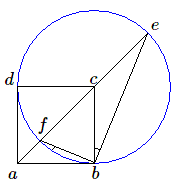
On a \(ac/ab = \sqrt 2\) et \(ae/ab=\sqrt 2 + 1\). Les triangles \(abe\) et \(afb\) sont semblables; en effet on a l'égalité des angles \(abf\) et \(cbe\) (par rotation d'1/4 de tour) et celle des angles \(cbe\) et \(ceb\) (triangle isocèle ayant pour côté le rayon du cercle). On en déduit que si l'on applique l'algorithme d'Euclide aux segments \(ae\) et \(ab\), on est conduit aux segments \(ab\) et \(af\) qui leur sont semblables. Dès lors l'algorithme ne se terminera jamais et \(\sqrt 2 + 1\), et par suite \(\sqrt 2\) sont irrationnels.

A propos de rectangles remarquables, signalons le format des papiers A4, 21 × 29.7 cm. Le problème était de trouver un format tel que la juxtaposition de deux rectangles donne un rectangle semblable au rectangle initial afin, par exemple, de pouvoir réaliser des photocopies en réduction. Si x désigne le rapport du grand côté au petit côté du rectangle cherché, on obtient de manière évidente la condition :

\[ 1/x=x/2 \]

d'où l'on déduit \(x=\sqrt 2\).

La construction d'un tel rectangle à partir d'un carré ABCD est évidente:

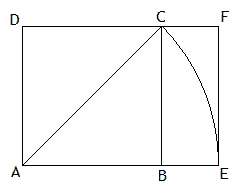
Le format A0 est défini comme un tel rectangle d'aire égale à \(1~m^2\); soit un petit côté de \(a~cm\); le grand côté \(b\) vaut \(a\sqrt 2~cm\). On a donc : \(a~cm × a\sqrt 2~cm = 1~m^2\). D'où, en centimètres, \(a=84,09...~~~\text{et}~~~b=118,92...\) Les autres formats sont obtenus en divisant chaque feuille en deux parties égales; en arrondissant, on obtient entre autres le format A4 \((21 × 29,7)\) qui divisé en deux donne le format A5 \((14,5 × 21)\) qui divisé à son tour donne le format A6 dit "carte postale" \(10,5 × 14.8\).

Les formats de la famille B sont également des rectangles de mêmes proportions. Le format B0 est défini par la dimension du plus petit côté qui vaut \(1m\) ; l'autre côté vaut \(1,414 m\). Ces papiers sont essentielement employés en imprimerie.