Archimède s'intéressa aux aires et volumes d'êtres géométriques. Il est célèbre pour sa détermination approchée de la valeur de \(\pi\) qu'il encadre par les valeurs 3 1/7 et 3 10/71. Il obtient ces valeurs à partir du calcul des périmètres de polygones inscrits et circonscrits à un cercle. Mais il calcula bien d'autres choses. En particulier il détermina le volume du cône et de la sphère. A l'heure actuelle ces résultats sont obtenus à l'aide du calcul intégral. Pourtant bien avant l'introduction de celui-ci, Cavalieri énonça un principe qui permettait de retrouver les résultats obtenus par Archimède.

Voyons comment plusieurs siècles plus tôt Archimède avait procédé.

Pour calculer le volume d'un cône, Archimède ne fait rien d'autre que d'utiliser la formule donnant le volume d'une pyramide de base \(B\) et de hauteur \(h\), soit \(1/3Bh\).

Comment arrive-t-on à cette formule?

Considérons un carré. Il est possible, en utilisant une diagonale, de le partager en 2 triangles égaux; l'aire de chacun d'eux vaut \(1/2Bh\).

De même, un cube peut, à l'aide d'une diagonale être partagé en 3 pyramides égales; le volume de chacune d'elles est \(1/3Bh\).

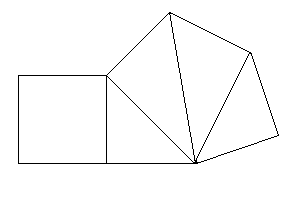Vous trouverez ci-contre le patron d'une de ces pyramides. Elle possède un carré de côté \(a\) et 4 faces triangulaires: 2 triangles rectangles isocèles de base \(a\sqrt{2}\) et deux autres triangles rectangles de côtés \(a, a\sqrt{2}\) et \(a\sqrt{3}\).

Attention ! En fait, nous ne prouvons la formule du volume de la pyramide \(V=1/3a^2\) que dans le cas où sa hauteur \(a\) est égale au côté du cube. Comment généraliser cette formule à une pyramide quelconque ? En remarquant deux choses:

• Si la hauteur est multipliée par un facteur k, le volume l'est également;
• Si les bases sont équivalentes, les volumes sont égaux.

Cette dernière propriété est connue sous le nom du principe de Cavalieri . Cette propriété bien connue des Grecs a été énoncée par Cavalieri et est actuellement démontrée à l'aide du calcul intégral. En fait, il suffit de s'imaginer deux volumes reposant sur un plan horizontal et découpés en fines tranches par une famille de plans horizontaux. Si les sections homologues sont équivalentes il est clair que les volumes sont égaux.

C'est en fait ce principe qu'Archimède utilisa pour calculer le volume d'une sphère Considérons une demi-sphère de rayon \(R\) reposant sur un plan \(\alpha \) sur ce même plan soit un cylindre de rayon \(R\) et de hauteur \(R\); à l'intérieur de ce cylindre plaçons un cône dont le sommet est situé au centre de la base et qui projette le cercle supérieur du cylindre.

Si nous sectionnons ces deux volumes par un plan horizontal situé à une hauteur \(x\), nous obtenons dans la sphère un cercle, et dans l'autre volume un anneau.

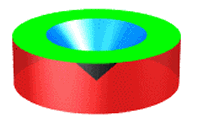
Calculons les aires de chacune des deux surfaces.

Tout d'abord le cercle, section dans la sphère. à l'aide du théorème de Pythagore , on voit que son rayon \(r\) satisfait à \(r^2+x^2=R^2\), d'où \(r^2=R^2-x^2\). L'aire de la section vaut donc \(\pi(R^2-x^2)\)

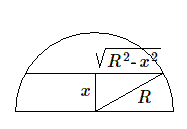
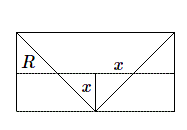
Passons à l'anneau. C'est la différence entre l'aire du cercle extérieur qui vaut \(\pi R^2\) et celle du cercle intérieur; ce dernier a pour rayon \(x\). On obtient ainsi l'aire de l'anneau: \(\pi R^2-\pi x^2\). Les sections par les plans horizontaux ont donc toujours même aire, et on en déduit que les volumes sont égaux. Par conséquent le volume de la demi-sphère équivaut à la différence entre celui du cylindre et celui du cône, c'est-à-dire \(\pi R^2.R - 1/3\pi R.R\) ou encore \(2/3\pi R^2\). Le volume de la sphère est donc égal à \(4/3\pi R^3\).

Connaissant le volume d'une sphère de rayon \(R\), il n'est guère difficile d'en trouver l'aire. Une variation du rayon entraîne une variation de volume égale, en première approximation au produit de l'aire de la sphère par la variation du rayon. Cette remarque nous montre, par une simple application de la définition de la dérivée (qu'Archimède appliquait il y a plus de 2000 ans), que l'aire de la sphère est égale à la dérivée de son volume par rapport au rayon \(R\) et vaut \(4\pi R^2\).