L'origami, au sens strict, consiste à utiliser une feuille de papier sans la découper ; la seule opération permise est le pliage dans un sens (montagne) ou dans l'autre (vallée). Il paraît, à première vue, impossible d'obtenir des formes courbes et pourtant ...

Voici un pliage extrêmement simple qui conduit à un paraboloïde hyperbolique . Cette surface est l'une des figures les plus simples rencontrée dans différents domaines.

À l'école primaire, on peut faire un graphique de la "table de multiplication". On prend pour base un quadrillage dessiné sur une plaque où il est possible de planter un bâtonnet (polystyrène expansé par exemple). Les enfants habitués au jeu de combat naval se débrouilleront sans peine dans le système de coordonnées. Chaque case est déterminée par deux informations, sa position horizontale et sa position verticale. Il suffit donc de numéroter les rangées et les colonnes, et chaque case sera repérée par deux nombres naturels. Dans la case choisie, on plante un bâtonnet dont la mesure, en centimètres, est égale au produit des deux nombres. Et voila un morceau de paraboloïde hyperbolique qui se crée. Algébriquement, il correspond à une portion du graphique de la fonction z = x*y , limité aux valeurs naturelles de x et y.

Par la suite, on passera aux entiers et on pourra aisément compléter le graphique.

Dans l'enseignement secondaire, le cours de physique étudie les lois des gaz parfaits (Charles, Gay-Lussac, Boyle-Mariotte) et cette fois les variables x, y, z sont des réels positifs correspondant respectivement à la pression au volume et à la température. À volume constant ou pression constante, on obtient la loi de Charles ou celle de Gay-Lussac représentées dans les plans x = x ₀ ou y = y ₀ par des droites ; la loi de Boyle-Mariotte sera décrite par des hyperboles situées dans les plans z = z ₀ à température constante.

Un autre rencontre avec le paraboloïde hyperbolique se passe lors de l'étude de la recherche du barycentre de 4 points massiques non coplanaires.

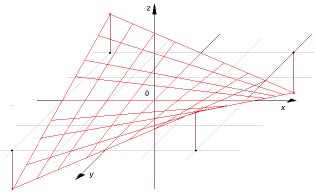
Dans un repère orthonormé, considérons le paraboloïde hyperbolique d'équation \(z = kxy\). Ses deux familles de droites sont données par les sections à \(x\) et \(y\) constants. En projetant orthogonalement dans le plan \(0xy\), on obtient deux familles de parallèles aux axes coordonnés. Parmi toutes les droites du plan \(z=0\), choisissons deux couples de droites symétriques délimitant un carré centré à l'origine de côté 2a. Les sommets ont pour coordonnées \((x, y) = (\pm a, \pm a)\). Ces quatre points auront donc pour coordonnée \(z, ka^2 \text{ou} -ka^2\) et délimitent un quadrilatère gauche. Partons d'un quadrilatère gauche possédant ces propriétés de symétrie. Il définit donc un unique paraboloïde. Les segments de droites s'appuyant sur deux côtés opposés ont une longueur variable; elle est maximum sur les côtés et minimum pour le segment joignant les milieux des côtés opposés.

Passons à l'origami et essayons de construire à l'aide d'un carré de papier un tel morceau de paraboloïde. Ses droites seront obtenues à l'aide des parallèles aux paires de côtés opposés. Toutefois, les segments de droites ne pourront pas être égaux ainsi que nous venons de le voir. La solution consiste à déformer par pliage ces segments. Voici la solution proposée.

Prenons une feuille de papier carrée et deux familles de droites parallèles aux côtés régulièrement espacées. Dessinons ensuite les carrés concentriques obtenus. Ces carrés seront pliés le long de leurs côtés alternativement en "montagne" et "vallée" selon le schéma ci-dessous. Nous dessinerons les montagnes en rouge et les vallées (évidemment) en vert !

Ce modèle une fois construit donne, par inclinaison des bords, différentes figures. On peut facilement montrer qu'elles sont toutes d'excellentes approximations de paraboloïdes hyperboliques.

Quelques conseils pratiques pour la réalisation de ce beau modèle.

• Tout d'abord, utilisez, vous l'aviez deviné, du papier quadrillé mais choisissez-le assez lourd (120g/m² minimum).
• Si possible reproduisez, éventuellement par transparence, le dessin sur les deux faces (il est plus facile de plier selon une "montagne" que selon une "vallée").
• En pliant, ne dépassez surtout pas la zone à plier ; si le papier est suffisamment solide, marquez le pli en pressant le dos d'un couteau.
• Enfin, pour la facilité, rigidifiez les 4 bandes latérales, soit en collant une double épaisseur ou, mieux, une mince baguette de bois (comme celles utilisées pour les brochettes).

Bon amusement.