Voilà une bonne question qui mérite mieux que la réponse traditionnelle : "On n'en sait rien, ceux qui sont allés voir là-bas ne sont toujours pas revenus !"

Tout le monde a entendu parler de "points à l'infini"; du moins en Belgique, car en France, on les appelle "points impropres", comme s'ils n'étaient pas bien lavés.

La question est pourtant bien intéressante. Elle s'est posée, il y a plus d'un demi-millénaire, lors de la Renaissance. A l'époque, les peintres se sont intéressés à la perspective et on a ainsi parlé de points "à l'infini"(*). Le plan horizontal était alors complété par ces points situés sur une droite appelée "ligne d'horizon".

(*)Sur les schémas qui suivent, les éléments "à l'infini" seront dessinés en rouge.

Une droite à l'infini

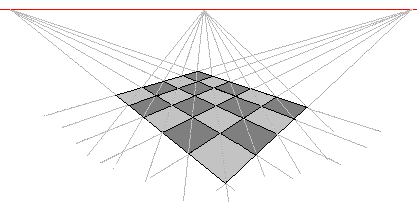Attardons-nous à cette première situation. Le problème était posé lors de la projection de la réalité spatiale sur un plan, le plan de la toile de l'artiste, à partir d'un point: l'œil du peintre. Celui-ci voyait les droites parallèles se rencontrer au loin en un point de l'horizon. Ainsi était né le plan projectif, ou plus généralement l' espace projectif , et la géométrie projective, extension de la géométrie affine ou linéaire.

Dans le plan, on avait deux propriétés, tellement importantes qu'on les choisissait généralement comme axiomes:

Toutefois, il y avait une exception : les deux droites pouvaient être parallèles. Mais cela n'arrivait pas souvent. D'ailleurs, Euclide qui avait rencontré la difficulté et avait ajouté son fameux cinquième postulat qui affirmait l'unicité de la parallèle. Pour les peintres, qui se moquaient évidemment d'Euclide et de ses postulats, cela posait un vrai problème. Lorsqu'il y avait deux parallèles, leurs yeux voyaient pourtant les deux droites se couper au loin. De là, naquit l'idée de compléter l'espace. Ici, nous nous limiterons au plan que nous compléterons par des nouveaux points "à l'infini" aux propriétés bien précises. Toutes les droites d'une même direction, autrement dit une famille de parallèles ont en commun un point à l'infini. De plus, tous ces points à l'infini sont alignés (sur la fameuse ligne d'horizon).

Pour les mathématiciens cette solution était très séduisante. En effet, si l'on complète le plan par les points d'une droite à l'infini, on peut alors énoncer les deux propriétés:

Et cette fois il n'y a plus aucune exception ! La géométrie projective était née mais il fallut encore attendre le XIXe siècle pour la voir prendre son essor.

Un point à l'infini

Une autre situation se présenta au début du XIXe. Les nombres complexes , eux aussi découverts à la Renaissance, suscitent l'intérêt de nombreux mathématiciens. Le Danois Caspar Wessel est le premier, en 1787, à donner une représentation géométrique des nombres complexes dans le plan (euclidien). Argand, Cauchy et Gauss utilisent également la même représentation géométrique des nombres complexes.

L'addition \(z\rightarrow z + b \) correspond à la translation de vecteur \(\vec{0b}\), la multiplication \(z\rightarrow az\) à une similitude centrée en 0. Le passage à l'inverse est la composée d'une inversion et d'une symétrie. Les éléments d'un corps possèdent classiquement tous un inverse; tous, à l'exception de 0. En algèbre, on peut mettre fin à cette exception en complétant le corps par un élément infini , \(\infty\). Il est donc logique d'adjoindre au plan un élément "à l'infini", un point \(\infty\). Cela se justifie car les applications \(z\rightarrow az+b\) correspondent aux similitudes directes du plan et \(z\rightarrow a\bar{z}+b\) aux similitudes indirectes. Ces transformations conservent les droites, les cercles et les angles. Après l'adjonction d'un point à l'infini, l' inversion , est devenue une permutation. Cependant, elle transforme parfois une droite en un cercle et vice-versa. En regroupant droites et cercles sous la même dénomination : "cycles", on peut dès lors affirmer que l'inversion est une permutation du plan complété qui conserve l'ensemble des cycles . Signalons que de plus elle conserve également les angles.

Certes, si le regroupement des droites (courbes du premier degré) et des cercles (courbes du second degré) peut heurter, à la réflexion, cela ne pose guère de problème. Au contraire; l'adjonction d'un (unique) point à l'infini au plan, point commun à toutes les droites, permet d'éviter des exceptions.

En effet, dans le plan 3 points distincts appartiennent à un unique cercle. Mais attention, il y a à nouveau exception si ces trois points sont alignés. Le regroupement droites et cercles permet d'affirmer que 3 points distincts appartiennent toujours à un unique cycle. De même si deux cycles ont un point commun, ils en possèdent un second, éventuellement confondu et dans ce cas, ils sont dits tangents. Bref, toutes ces exceptions, tant algébriques que géométriques, disparaissent.

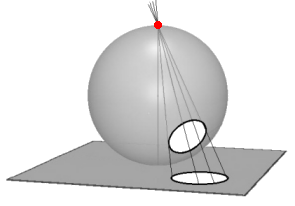Le nouveau plan, plan complété par un point à l'infini, est appelé plan conforme ou encore sphère de Riemann. Il suffit de penser à la projection stéréographique d'une sphère sur un plan pour voir qu'on évite l'exception du centre de projection qui n'a pas d'image; il correspond tout simplement au point à l'infini. La géométrie associée est la géométrie conforme.

Ce plan est très proche d'une géométrie non-euclidienne. En effet, si on identifie sur la sphère les paires de points antipodes et on arrive alors à la géométrie "elliptique". Les points sont les paires de points antipodes et les droites les grands cercles . On vérifie sans peine que sur une sphère:

Il n'y a donc pas de parallèle, le postulat d'Euclide est nié.

Une conique ou un cercle à l'infini

Toutefois, il existe une autre manière de rejeter ce postulat en supposant que, par un point extérieur à une droite, il existe plusieurs parallèles (non-sécantes). Historiquement, c'est ce cas qui a été étudié en premier lieu. La géométrie "hyperbolique" est le résultat des travaux de Lobatchevski, Bolyay et Gauss.

Soit, dans un tel plan, une droite (que, pour des facilités de langage, nous supposerons horizontale) et un point extérieur. Partons d'une des sécantes. Lorsque le point d'intersection avec l'horizontale s'éloigne, soit vers la droite, soit vers la gauche, la droite pivotera et cessera à un certain moment de couper l'horizontale. Comme on suppose que la parallèle n'est plus unique, on aura une parallèle à droite et une autre à gauche. Dans l'angle formé par ces deux parallèles "limites", toutes les droites seront des non-sécantes. Tout comme en analyse, on complète les réels par deux éléments +\(\infty\) et -\(\infty\), il est donc logique de compléter la droite par deux points à l'infini: l'un "à droite" et l'autre "à gauche". Toutes les droites seront complétées de la même manière.

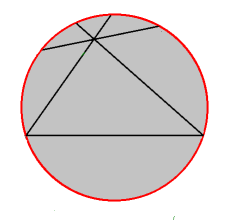
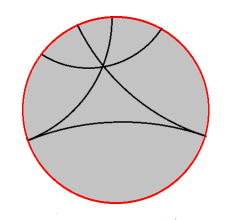L'ensemble des points à l'infini formera une courbe convexe que l'on peut représenter par un cercle.

Cela conduit à deux modèles de la géométrie hyperbolique . Le premier, intérieur d'une conique d'un plan projectif, où les droites sont les segments intérieurs, a été utilisé par Félix Klein. Le second, le demi plan complexe, où les droites sont des demi-cercles orthogonaux à l'axe réel, par Henri Poincaré.

Et autre chose itou

En résumé, nous avons vu qu'un plan peut être complété de diverses manières: une doite, un point, une courbe ovale. Il existe encore d'autres possibilités et notamment, dans le cas d'un plan de la relativité , une complétion par une paire de sécantes, ce qui lui donne une structure de quadrique réglée.

Il est évidement que toute complétion n'est pas arbitraire et doit pouvoir être justifiée par un souci de simplification lors de l'étude de certaines propriétés.