Soit \(Z = Z(z)\) une fonction dérivable de la variable complexe \(z=x+iy\). Le nombre complexe \(Z\) peut s'écrire \(X+iY\). La fonction qui applique \(z\) sur \(Z\) se ramène à un couple de 2 fonctions réelles de 2 variables \(X=X(x,y), Y=Y(x,y)\).

Géométriquement, on a une application du plan \(p\) de la variable \(z\) vers le plan \(P\) de la variable \(Z\).

\(Z\) est fonction d'une variable complexe \(z\) ; comment calculer cette dérivée ? Pour se ramener au cas de la dérivée d'une fonction d'une seule variable, il y a deux manières particulièrement simples d'y arriver. On peut imaginer deux cas particuliers :

• seule la partie réelle de \(z\) varie et, dans ce cas, \(x\) varie mais \(y\) reste constant
• seule la partie imaginaire de \(z\) varie et, dans ce cas, \(x\) reste constant et \(y\) varie.

Considérons tout d'abord, le cas où seul \(x\) varie. La fonction \(Z=X+iY\) est alors une fonction d'une variable réelle et on peut obtenir la dérivée en prenant la dérivée de \(X\) plus \(i\) fois la dérivée de \(Y\). Dans le second cas, on peut procéder d'une manière analogue en calculant les dérivées des fonctions \(X\) et \(Y\) par rapport à \(y\). En fin de compte, il y aura 4 dérivées ! Pour éviter les confusions, on introduit une nouvelle terminologie ainsi qu'une nouvelle notation.

Dans chacune des dérivées dont nous avons parlé, on n'utilise qu'une partie des variables, on dit qu'il s'agit de dérivées partielles. Concrètement, si nous dérivons \(X\) par rapport à \(x\) en supposant que \(y\) est constant, on dira qu'il s'agit de la dérivée partielle de \(X\) par rapport à \(x\) . Elle sera notée :

\[ \frac{\partial X}{\partial x} \]

Nous disposons donc d'une nouvelle notation qui permettra d'écrire les deux manières de dériver la fonction \(Z\) :

\[ \begin{cases} \large \frac{dZ}{dx}=\frac{\partial X}{\partial x}+i\frac{\partial Y}{\partial x}\\ \large \frac{dZ}{dy}=\frac{\partial X}{\partial y}+i\frac{\partial Y}{\partial y} \end{cases} \]

Améliorons cela en remplaçant la dérivation par rapport à \(y\) par la dérivation par rapport à la partie imaginaire \(iy\). Rien de plus simple : il suffit de diviser la dérivée partielle par rapport à \(y\) par le nombre \(i\) ou tout simplement de multiplier par son inverse \(-i\). On obtient :

\[ \frac{dZ}{diy}=-i\frac{dZ}{dy}=-i\frac{\partial X}{\partial y}+\frac{\partial Y}{\partial y} \]

La fonction \(Z\) sera dérivable en un point si la dérivée ne dépend pas du chemin suivi. En particulier la dérivée dans une direction réelle, par rapport à \(x\), doit être égale à la dérivée dans une direction imaginaire pure, c'est-à-dire par rapport à \(y\). Par comparaison des deux valeurs, on obtient en égalant les parties réelles et imaginaires :

\[ \begin{cases} \large \frac{\partial X}{\partial x}= ~~~  \frac{\partial Y}{\partial y} \\ \large \frac{\partial X}{\partial y}= -\frac{\partial Y}{\partial x} \end{cases}\]

Les deux fonctions \(X\) et \(Y\) ne sont donc pas quelconques; elles satisfont à ces relations appelées équations de Cauchy - Riemann .

Quelles en sont les conséquences ?

Si, dans le plan \(p (x,y)\) nous avons une courbe \(c\) d'équations \(x=x(t)~~\text{et}~~y=y(t)\), son image dans le plan \(P (X,Y)\) est la courbe \(C\) d'équations: \(X=X(x(t),y(t)),~Y=Y(x(t),y(t))\). Le vecteur tangent à \(C\) s'écrit:

\[ \begin{cases} \large \frac{dX}{dt}=\frac{\partial X}{\partial x}\frac{dx}{dt}+\frac{\partial X}{\partial y}\frac {dy}{dt} \\ \large \frac{dY}{dt}=\frac{\partial Y}{\partial x}\frac{dx}{dt}+\frac{\partial Y}{\partial y}\frac{dy}{dt} \end{cases} \]

Il est donc l'image du vecteur tangent à la courbe \(c~(dx/dt, dy/dt)\) par l'application dont la matrice est:

\[ \left\lgroup\matrix{ ~\large \frac{\partial X}{\partial x} & \large \frac{\partial X}{\partial y}\\ ~\large \frac{\partial Y}{\partial x} & \large \frac{\partial Y}{\partial y}} \right\rgroup \]

Mais grâce aux équations de Cauchy-Riemann, nous voyons que cette matrice est du type:

\[ \left\lgroup\matrix{a & b\\-b & a}\right\rgroup \]

c'est-à-dire une matrice de similitude . En particulier les angles formés par les directions en un point sont conservés; dans ces conditions, les transformations de \(p\) vers \(P\) sont dites transformations conformes.

Des courbes orthogonales sont appliquées sur des courbes orthogonales et en particulier les réseaux de courbes \(x=x_0,y=y_0\) du plan \(p\) ou \(X=X_0,Y=Y_0\) du plan \(P\). Notons enfin que les fonctions \(X(x,y)\) et \(Y(x,y)\) sont dites harmoniques; elles satisfont à l'équation:

\[ \frac{\partial^2 X}{\partial x^2}+\frac{\partial^2 Y}{\partial y^2}=0 \]

Etudions à titre d'exemple la fonction appliquant \(z\) sur son carré \(Z\); on a:

\[ Z = X + iY = (x + iy)^2 = x^2 - y^2 + 2 ixy \]

La relation entre \(z\) et \(Z\) n'est pas bijective; \(z_0\) et \(-z_0\) ont même carré. Deux points symétriques par rapport à l'origine dans le plan de la variable z correspondent à un même point du plan de la fonction \(Z\). Si on désire avoir une bijection, il faut donc limiter le domaine de \(z\) à un demi-plan limité par une demi-droite. On pourrait également continuer à étudier l'application du plan entier de la variable \(z\) mais alors l'image serait formée de deux copies connectées du plan des \(Z\), la surface de Riemann associée à la fonction carré.

Les droites \(x=x_0\) donnent les courbes:

\(\begin{cases} X={x_0}^2-y^2\\Y=2{x_0}y\end{cases}\)

c'est-à-dire des paraboles: \(X={x_0}^2-(Y/2{x_0})^2\)

et les droites \(y=y_0\) donnent les courbes:

\(\begin{cases} X=x^2-{y_0}^2\\Y=2x{y_0}\end{cases}\)

c'est-à-dire des paraboles: \( X=(Y/2{y_0})^2-{y_0}^2\)

Ces deux familles de paraboles sont orthogonales:

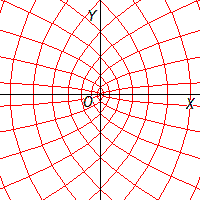
L'image du réseau orthogonal des courbes \(x=x_0~~\text{et}~~y=y_0\) est le réseau orthogonal formé par ces deux familles de paraboles.

Les choses se visualisent fort bien si l'on considère l'application qui envoie \(z\) sur une combinaison linéaire de \(z\) et de \(Z=z^2\) ; les deux réseaux de droites orthogonales \(x\) et \(y\) constants sont envoyés sur les deux réseaux de paraboles orthogonales. De manière plus précise, on applique \(z\) sur \((1-\lambda)z+\lambda z^2\) avec\(\lambda\) variant de \(0\) à \(1\).

De même, dans le plan \(P\) de la variable \(Z\), les courbes \(X=X_0\) et \(Y=Y_0\) proviennent des courbes:

\[ \begin{cases} x^2-y^2=X_0\\2xy=Y_0\end{cases} \]

c'est-à-dire de 2 familles d'hyperboles équilatères ayant pour asymptotes respectivement les bissectrices des axes et les axes eux-mêmes. Ces deux réseaux d'hyperboles du plan de la variable \(z\) sont l'image des réseaux de droites coordonnées du plan \(Z\).

On peut considérer la relation réciproque entre \(Z\) et \(z\) ; \(z\) une racine carrée de \(Z\). On pourrait obtenir une fonction en se limitant à la racine carrée "positive", c'est-à-dire celle dont la partie réelle est positive ou, si celle-ci est nulle, la partie imaginaire positive mais cela n'a guère de sens car le corps des complexes n'est pas ordonné.

En fait, la relation de \(Z\) vers \(\sqrt{Z}\) est une fonction multiforme : tout complexe \(Z\) a pour image deux complexes opposés, \(z\) et \(-z\) ou, vu géométriquement, deux points symétriques par rapport à l'origine.

Cette fonction, qui applique \(Z\) sur ses racines carrées, transforme les deux réseaux des droites orthogonales \(X=P\) et \(Y=Q\) en les deux réseaux orthogonaux d'hyperboles équilatères.

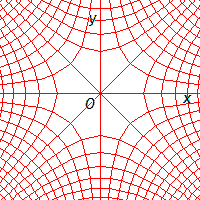
Comme plus haut, on peut visualiser cette application de manière dynamique en considérant l'application de \(Z\) sur une combinaison linéaire de \(Z\) et de \(z=\sqrt{Z}\) . De manière plus précise, on applique \(Z\) sur \((1- \lambda)Z+\lambda \sqrt{Z}\) avec \(\lambda \) variant de \(0\) à \(1\).

On peut procéder de même pour d'autres fonctions d'une variable complexe, par exemple les familles de courbes associées à l'élévation aux puissances entières ou celles associées à des fonctions transcendantes, en particulier aux fonctions \(\mathbf{sin~}z\) et \(\mathbf{exp~}z\) .