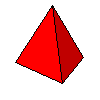
Famille du tétraèdre
(kaléidoscope: angles de \(π/2,π/3,π/3\))
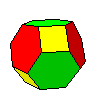
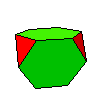
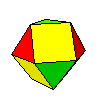
Le polyèdre générique est engendré par les 24 images d'un point quelconque sous l'action des 24 isométries du tétraèdre . Ce polyèdre n'est, en général, pas régulier ni semi-régulier. Les faces sont des polygones semi-réguliers. Toutefois, en partant de certains points "bien choisis", on peut obtenir les polyèdres réguliers et semi-réguliers.
Deux remarques:
- tout d'abord, étant donné la symétrie du kaléïdoscope associé, les polyèdres à droite du schéma sont les mêmes que les polyèdres à gauche;
- ensuite les polyèdres situés sur la verticale du schéma appartiennent à la famille du cube: ils s'en distinguent par le groupe d'automorphismes, deux faces hexagonales ou triangulaires adjacentes doivent être considérées comme faisant partie de deux familles distinctes.
En utilisant la souris sur l'image vous pourrez manipuler le polyèdre choisi.

|

|
|
|
|
|

|